הרצאה בנושא "בדיקת ניצב של שני מישורים"
הרעיון של מטוס בחלל מאפשר לנו להשיג, למשל, את פני השטח של שולחן או קיר. עם זאת, לשולחן או לקיר יש ממדים סופיים, והמישור משתרע מעבר לגבולותיו עד אינסוף.שקול שני מישורים מצטלבים. כאשר הם מצטלבים, הם יוצרים ארבע זוויות דו-הדרליות עם קצה משותף.
בואו נזכור מהי זווית דיהדרלית.
במציאות אנו פוגשים חפצים בעלי צורה של זווית דיהדרלית: למשל דלת פתוחה מעט או תיקייה פתוחה למחצה.

כאשר שני מישורים אלפא ובטא מצטלבים, נקבל ארבע זוויות דו-הדרליות. תן לאחת מהזוויות הדו-הדרליות להיות שווה ל- (phi), ואז השנייה שווה ל- (180 0 –), שלישי, רביעי (180 0 -).

α וβ, 0°< 90 °
שקול את המקרה כאשר אחת מהזוויות הדו-הדרלית היא 90 0 .
לאחר מכן, כל זוויות הדיהדרליות במקרה זה שוות ל-90 0 .
זווית דיהדרלית בין מישוריםα וβ,
90º
הבה נציג את ההגדרה של מישורים מאונכים:
שני מישורים נקראים מאונכים אם הזווית הדו-הדרלית ביניהם היא 90°.
הזווית בין מטוסי הסיגמה והאפסילון היא 90 מעלות, כלומר המישורים מאונכים
כי =90°
הבה ניתן דוגמאות של מישורים מאונכים.
קיר ותקרה.
קיר צד ופלטת שולחן.

קיר ותקרה
הבה ננסח סימן של ניצב של שני מישורים:
מִשׁפָּט:אם אחד משני מישורים עובר דרך קו מאונך למישור השני, אז המישורים הללו מאונכים.
בואו נוכיח את הסימן הזה.
לפי תנאי ידוע שהקו הישרAM נמצא במישור α, הקו הישר AM מאונך למישור β,
הוכח: מישורים α ו-β מאונכים.
הוכחה:
1) מישורים α וβ מצטלבים לאורך הישר AR, ו-AM AR, שכן AM β לפי תנאי, כלומר, AM מאונך לכל ישר השוכן במישור β.
2) הבה נצייר קו ישר במישור βאT מאונךאר.
נקבל את הזווית TאM היא הזווית הליניארית של הזווית הדו-הדרלית. אבל זווית TאM = 90°, מכיוון ש-MA הוא β. אז α β.
Q.E.D.
מִשׁפָּט:אם מישור עובר דרך קו מאונך למישור אחר, אז המישורים הללו מאונכים.

נָתוּן:α, β, AM α, AMβ, AM∩=A
הוכח: αβ.
הוכחה:
1) α∩β = AR, בעוד AM AR, שכן AM β לפי תנאי, כלומר, AM מאונך לכל קו ישר השוכן במישור β.
2) ATβ,אטאר.
TAM היא הזווית הליניארית של הזווית הדו-הדרלית. TAM = 90°, כי MA β. אז α β.
Q.E.D
מסימן הניצב של שני מישורים יש לנו תוצאה חשובה:
פְּגִיעָה:מישור מאונך לישר שלאורכו מצטלבים שני מישורים מאונך לכל אחד מהמישורים הללו.
הבה נוכיח את המסקנה הזו: אם מישור הגמא מאונך לישר c, אזי, בהתבסס על המקבילות של שני המישורים, גמא מאונך לאלפא. כמו כן, גמא מאונך לבטא

כלומר: אם α∩β=с ו-γс, אז γα ו-γβ.
כיγс ו-сα מסימן הניצב γα.
דומה ל-γβ
הבה ננסח מחדש את המסקנה הזו לזווית דו-הדרלית:
המישור העובר דרך הזווית הליניארית של זווית דו-הדרלית מאונך לקצה ולפנים של זווית דו-הדרלית זו. במילים אחרות, אם בנינו זווית לינארית של זווית דו-הדרלית, אזי המישור העובר דרכה מאונך לקצה ולפנים של זווית דו-הדרלית זו.

מְשִׁימָה.
נתון: ΔАВС, С = 90°, АС נמצאת במישור α, הזווית בין המישורים α וא ב ג= 60°, AC = 5 ס"מ, AB = 13 ס"מ.
מצא: המרחק מנקודה B למישור α.
פִּתָרוֹן:
1) בואו נבנה את VC α. אז KS היא הקרנת השמש על המישור הזה.
2) BC AC (לפי תנאי), כלומר, לפי משפט שלושת הניצבים (TPP), KS AC. לכן, VSK היא הזווית הליניארית של הזווית הדו-הדרלית בין המישור α למישור המשולש ABC. כלומר, VSK = 60°.
3) מ-ΔBCA לפי משפט פיתגורס:
מ-ΔVKS: ![]()
שיעור זה יעזור לאלה המעוניינים להבין את הנושא "סימן הניצב של שני מישורים". בתחילתו נחזור על ההגדרה של זוויות דו-הדרליות וליניאריות. לאחר מכן נשקול אילו מישורים נקראים בניצב, ונוכיח את סימן הניצב של שני מישורים.
נושא: ניצב של קווים ומישורים
שיעור: סימן הניצב של שני מישורים
הַגדָרָה. זווית דיהדרלית היא דמות שנוצרת על ידי שני חצאי מישורים שאינם שייכים לאותו מישור והקו הישר המשותף שלהם a (a הוא קצה).
אורז. 1
הבה ניקח בחשבון שני חצאי מישורים α ו-β (איור 1). הגבול המשותף שלהם הוא l. נתון זה נקרא זווית דיהדרלית. שני מישורים מצטלבים יוצרים ארבע זוויות דו-הדרליות עם קצה משותף.
זווית דיהדרלית נמדדת לפי הזווית הליניארית שלה. אנו בוחרים נקודה שרירותית על הקצה המשותף l של הזווית הדו-הדרלית. בחצי המישורים α ו-β, מנקודה זו אנו מציירים אנכים a ו-b לישר l ומקבלים את הזווית הליניארית של הזווית הדו-הדרלית.
קווים ישרים a ו-b יוצרים ארבע זוויות שוות ל-φ, 180° - φ, φ, 180° - φ. נזכיר שהזווית בין קווים ישרים היא הקטנה מבין הזוויות הללו.
הַגדָרָה. הזווית בין מישורים היא הקטנה ביותר מבין הזוויות הדו-הדרליות שנוצרות על ידי מישורים אלו. φ היא הזווית בין המישורים α ו-β, if
הַגדָרָה. שני מישורים מצטלבים נקראים בניצב (מאונך הדדי) אם הזווית ביניהם היא 90°.

אורז. 2
נקודה שרירותית M נבחרה על קצה l (איור 2). הבה נצייר שני קווים ישרים מאונכים MA = a ו-MB = b לקצה l במישור α ובמישור β, בהתאמה. קיבלנו את הזווית AMB. זווית AMB היא הזווית הליניארית של זווית דו-הדרלית. אם הזווית AMB היא 90°, אז המישורים α ו-β נקראים מאונכים.
קו b מאונך לקו l לפי בנייה. קו b מאונך לישר a, מכיוון שהזווית בין המישורים α ו-β היא 90°. אנו מוצאים שישר b מאונך לשני ישרים מצטלבים a ו-l מהמישור α. המשמעות היא שהישר b מאונך למישור α.
באופן דומה, אנו יכולים להוכיח כי הישר a מאונך למישור β. קו a מאונך לקו l לפי בנייה. קו a מאונך לישר b, מכיוון שהזווית בין המישורים α ו-β היא 90°. אנו מוצאים שהישר a מאונך לשני ישרים חוצים b ו-l מהמישור β. המשמעות היא שהישר a מאונך למישור β.
אם אחד משני מישורים עובר דרך קו מאונך למישור השני, אז מישורים כאלה הם מאונכים.
לְהוֹכִיחַ:

אורז. 3
הוכחה:
תנו למטוסים α ו-β להצטלב לאורך קו ישר AC (איור 3). כדי להוכיח שהמישורים מאונכים זה לזה, צריך לבנות זווית לינארית ביניהם ולהראות שהזווית הזו היא 90°.
הישר AB מאונך למישור β, ולכן לישר AC השוכן במישור β.
הבה נצייר קו ישר AD מאונך לישר AC במישור β. אז BAD היא הזווית הליניארית של הזווית הדו-הדרלית.
הישר AB מאונך למישור β, ולכן לישר AD השוכן במישור β. המשמעות היא שהזווית הליניארית BAD היא 90°. זה אומר שהמישורים α ו-β מאונכים, וזה מה שהיה צריך להוכיח.
המישור הניצב לישר שלאורכו מצטלבים שני מישורים נתונים מאונך לכל אחד מהמישורים הללו (איור 4).
לְהוֹכִיחַ:

אורז. 4
הוכחה:
הישר l מאונך למישור γ, והמישור α עובר דרך הישר l. המשמעות היא שבהתבסס על הניצב של מישורים, המישורים α ו- γ מאונכים.
הישר l מאונך למישור γ, והמישור β עובר דרך הישר l. המשמעות היא שלפי הניצב של מישורים, המישורים β ו-γ מאונכים.
הַגדָרָה.זווית דיהדרלית היא דמות שנוצרת על ידי קו ישר a ושני חצאי מישורים בעלי גבול משותף a, ואינם שייכים לאותו מישור.
הַגדָרָה.מידת המעלות של זווית דיהדרלית היא מידת המעלות של כל אחת מהזוויות הליניאריות שלה.
הַגדָרָה.שני מישורים מצטלבים נקראים בניצב אם הזווית ביניהם היא 90 o.
סימן לניצב של שני מישורים.
נכסים.
- בקוביד, כל ששת הפנים הם מלבנים.
- כל הזוויות הדו-הדרליות של קוביד הן זוויות ישרות
- ריבוע האלכסון של מקבילי מלבני שווה לסכום הריבועים של שלושת ממדיו.
בעיות ומבחנים בנושא "נושא 7. "זווית דיהדרלית. ניצב של מטוסים."
- זווית דיהדרלית. ניצב של מטוסים
- ניצב של קו ומישור - ניצב קווים ומישורים, דרגה 10
שיעורים: 1 מטלות: 10 מבחנים: 1
- מאונך ואלכסוני. זווית בין קו ישר למישור - ניצב קווים ומישורים, דרגה 10
שיעורים: 2 מטלות: 10 מבחנים: 1
- מקביליות של מטוסים - מקביליות קווים ומטוסים, דרגה 10
שיעורים: 1 מטלות: 8 מבחנים: 1
- קווים מאונכים - מידע גיאומטרי בסיסי כיתה ז'
שיעורים: 1 מטלות: 17 מבחנים: 1
החומר בנושא מסכם ומסדר את המידע שאתם מכירים מהפלנימטריה על הניצב של קווים ישרים. רצוי לשלב את חקר משפטים על הקשר בין מקבילות וניצב של קווים ישרים ומישורים במרחב, וכן חומר על הניצב והנוטה, עם חזרה שיטתית של החומר המקביל מהפלנימטריה.
פתרונות כמעט לכל בעיות החישוב מסתכמים ביישום משפט פיתגורס והשלכותיו. בבעיות רבות, האפשרות להשתמש במשפט פיתגורס או בהשלכותיו מוצדקת במשפט של שלושה ניצבים או בתכונות המקבילות והניצב של מישורים.
הרעיון של מישורים מאונכים
כששני מישורים מצטלבים, נקבל זוויות דיהדרליות של $4$. שתי זוויות שוות ל-$\varphi $, והשתיים האחרות שוות ל-$(180)^0-\varphi $.
הגדרה 1
הזווית בין מישורים היא המינימום של הזוויות הדו-הדרליות שנוצרות על ידי מישורים אלה.
הגדרה 2
שני מישורים מצטלבים נקראים בניצב אם הזווית בין המישורים הללו היא $90^\circ$ (איור 1).
איור 1. מישורים בניצב
סימן של ניצב של שני מישורים
משפט 1
אם קו ישר של מישור מאונך למישור אחר, אז המישורים הללו מאונכים זה לזה.
הוכחה.
נותנים לנו מישורים $\alpha $ ו-$\beta $, שמצטלבים לאורך הישר $AC$. תנו לקו הישר $AB$ המונח במישור $\alpha $ להיות מאונך למישור $\beta $ (איור 2).

איור 2.
מכיוון שהקו $AB$ מאונך למישור $\beta$, הוא גם מאונך לישר $AC$. הבה נצייר בנוסף קו $AD$ במישור $\beta$, בניצב לישר $AC$.
אנו מוצאים שהזווית $BAD$ היא הזווית הליניארית של הזווית הדו-הדרלית, שווה ל-$90^\circ$. כלומר, בהגדרה 1, הזווית בין המישורים היא $90^\circ$, מה שאומר שהמישורים הללו מאונכים.
המשפט מוכח.
המשפט הבא נובע ממשפט זה.
משפט 2
אם מישור מאונך לישר שלאורכו מצטלבים שני מישורים אחרים, אז הוא גם מאונך למישורים הללו.
הוכחה.
תנו לנו שני מישורים $\alpha $ ו-$\beta $ מצטלבים לאורך הישר $c$. המישור $\gamma $ מאונך לישר $c$ (איור 3)

איור 3.
מכיוון שהקו $c$ שייך למישור $\alpha $ והמישור $\gamma $ מאונך לישר $c$, אז לפי משפט 1, המישורים $\alpha $ ו-$\gamma $ מאונכים.
מכיוון שהקו $c$ שייך למישור $\beta $ והמישור $\gamma $ מאונך לישר $c$, אז לפי משפט 1, המישורים $\beta $ ו-$\gamma $ מאונכים.
המשפט מוכח.
עבור כל אחד מהמשפטים הללו, גם ההצהרות ההפוכות נכונות.
דוגמאות לבעיות
דוגמה 1
תנו לנו לקבל מקבילית מלבני $ABCDA_1B_1C_1D_1$. מצא את כל זוגות המישורים הניצבים (איור 5).

איור 4.
פִּתָרוֹן.
לפי ההגדרה של מישורים מקבילים ומניצבים מלבני, אנו רואים את שמונת זוגות המישורים הבאים מאונכים זה לזה: $(ABB_1)$ ו-$(ADD_1)$, $(ABB_1)$ ו-$(A_1B_1C_1)$, $( ABB_1)$ ו-$(BCC_1) $, $(ABB_1)$ ו-$(ABC)$, $(DCC_1)$ ו-$(ADD_1)$, $(DCC_1)$ ו-$(A_1B_1C_1)$, $(DCC_1) $ ו-$(BCC_1)$, $(DCC_1)$ ו-$(ABC)$.
דוגמה 2
תנו לנו שני מישורים ניצבים זה לזה. מנקודה במישור אחד נמשך מאונך למישור אחר. הוכיחו שהקו הזה נמצא במישור הנתון.
הוכחה.
נותנים לנו מישורים מאונכים $\alpha $ ו-$\beta $ המצטלבים לאורך הישר $c$. מנקודה $A$ של המישור $\beta $ נמשך $AC$ מאונך למישור $\alpha $. הבה נניח ש$AC$ אינו שוכב במישור $\beta$ (איור 6).
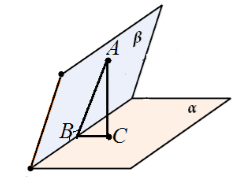
איור 5.
שקול משולש $ABC$. הוא מלבני עם זווית ישרה $ACB$. לכן, $\angle ABC\ne (90)^0$.
אבל מצד שני, $\angle ABC$ היא הזווית הליניארית של הזווית הדו-הדרלית שנוצרת על ידי מישורים אלה. כלומר, הזווית הדו-הדרלית שנוצרת על ידי מישורים אלו אינה שווה ל-90 מעלות. אנו מוצאים שהזווית בין המישורים אינה שווה ל-$90^\circ$. סְתִירָה. לכן, $AC$ נמצא במישור $\beta$.
בנייה של שני מישורים ניצבים זה לזה.כידוע, מישורים מאונכים אם ישר השייך למישור אחד מאונך למישור אחר.לכן, מישור מאונך לנתון יכול להימשך דרך קו מאונך למישור נתון, או מאונך לישר השוכן במישור נתון.
מוצג באיור. 4.12 מישורים (מישור משולש ABC ומישור P) מאונכים זה לזה, שכן מישור P מאונך לישר A1 השוכן במישור המשולש. ההקרנה של המישור P העובר דרך הקו עם ההקרנות m 2 n 2, m 1 n 1 ומאונך למישור המצוין על ידי ההקרנות a 2 b 2 c 2, a 1 b 1 c 1 של המשולש מוצגת ב תאנה. 4.12.
בנייה: 1. צייר את הקווים הראשיים של המטוס, C1 - אופקי, C2 - חזיתי.
2. דרך נקודה שרירותית E (הממוקמת מחוץ למשולש ABC), צייר קו ישר EF בניצב לקווים הראשיים של המישור (c 2 f 2 מאונך ל-c 2 2 2 ו-c 1 f 1 מאונך ל-1 1 1).
3. דרך נקודה N, צייר קו ישר שרירותי EM החותך עם EF, נקבל מישור P המוגדר על ידי שני ישרים חותכים (EM X EF).
לפיכך, המישור P(ME X EF) מאונך למישור Q(משולש ABC).
יש לציין כי עבור מישורים ניצבים זה לזה במיקום כללי, עקבותיהם באותו השם לעולם אינם מאונכים. אבל אם אחד מהמישורים הנתונים (או שניהם) הוא מישור כללי, אז הניצב ההדדי בתרשים של זוג אחד מהעקבות שלהם מציין את הניצב של המישורים במרחב.
18) ניתן לקבוע את קו החיתוך הישר של שני מישורים לפי שתי הנקודות המשותפות שלהם. לשם כך, קבע את נקודות החיתוך של כל שני ישרים של מישור אחד עם מישור אחר או נקודות החיתוך של ישר בכל אחד מהמישורים עם מישור אחר
רצף בנייה:
ניתן למצוא את קו החיתוך של שני מישורים על ידי שימוש במישורי חיתוך עזר בעת הפתרון. בדרך כלל נבחרים מטוסי הקרנה (לעיתים קרובות אופקיים או חזיתיים)
בחר מישור עזר אופקי שרירותי Ф1 הוא חותך את המישורים הנתונים לאורך קווים ישרים (12 ו-34) אשר (ב-p1 מצטלבים בנקודה k)
המישור האופקי השני חוצה את המישורים הנתונים גם לאורך האופקים, הם מצטלבים בנקודה E
ישר KE הוא קו החיתוך של מישורים נתונים.
הבה נשקול את הפתרון לבעיה זו על ציור שטוח.
שלב 1 של פתרון לבניית נקודה M, נעשה שימוש במישור הבולט אופקית - המתווך ("), המקיף את הצלע AB של משולש ABC.
שלב 2 של הפתרון אנו בונים את קו החיתוך (בציור הוא מצויין בנקודות 1 ו-2) של מישור הביניים (") ושל מישור DEK.
שלב 3 של הפתרון מצא את נקודת החיתוך M של קו 1 - 2 עם קו AB.
נמצאה נקודה M אחת של קו החיתוך הרצוי.
כדי לבנות את הנקודה N, נעשה שימוש במישור הבולט אופקית ("), המקיף את הצלע AC של משולש ABC.
הקונסטרוקציות דומות לקודמות.
קביעת הראות במישור H מתבצעת באמצעות נקודות מתחרות אופקית 4 ו-8
נקודה 4 ממוקמת מעל נקודה 8 (4" ו-8"), כך שבמישור H חלק המשולש DEK, הממוקם לכיוון נקודה 4, מכסה את חלקו של המשולש ABC, הממוקם מקו החיתוך לכיוון נקודה 8. בעזרת נקבע זוג של נקודות מתחרות חזיתית 6 ו-7 במישור V.

הצטלבות של שני מישורים הבולטים חזיתית (?)
ההצטלבות של שני מישורים הבולטים אופקית (?)
19) חיתוך הוא דימוי של חפץ מנותח נפשית על ידי מישור אחד או יותר, בעוד שהנתיחה המנטלית של חפץ מתייחסת רק לחיתוך זה ואינה גוררת שינוי בתמונות אחרות של אותו חפץ. הקטע מראה מה נמצא במישור החיתוך ומה נמצא מאחוריו.
בהתאם למספר מטוסי הגזירה, הקטע מחולק ל:
פשוט (עם מטוס חיתוך אחד)
מורכב (עם מספר מישורי חיתוך)
בהתאם למיקום מישור החיתוך ביחס למישור ההקרנה האופקי, החלקים מחולקים ל:
אופקי – מישור החיתוך מקביל למישור ההקרנה האופקי
אנכי - מישור החיתוך מאונך למישור ההקרנה האופקי
OBLIQUE - מישור חיתוך הוא איזו זווית עקיפה עם מישור אופקי =) קטע אנכי נקרא חֲזִיתִיאם מישור החיתוך מקביל למישור ההקרנות הקדמי. ו פּרוֹפִילאם מישור החיתוך מקביל למישור הפרופיל של הקרנות.
חיתוכים מורכבים הם LONGITUDINAL אם מטוסי החיתוך מכוונים לאורך או לגובה האובייקט. ולרוחב אם מטוסי החיתוך מכוונים בניצב לאורך או לגובה האובייקט.
STEP - אם מטוסי הגזירה מקבילים זה לזה
BROKEN - אם מטוסי החיתוך מצטלבים זה את זה.
חיתוכים מקומיים משמשים לחשוף את המבנה הפנימי של אובייקט במקום מוגבל נפרד. הקטע LOCAL SECTION מודגש בנוף בקו מוצק, גלי ודק.
ייעוד חתכים - מיקום מישור החיתוך מסומן בקו חתך פתוח. משיכות ההתחלה והסיום של קו החתך לא צריכות לחצות את קווי המתאר של התמונה המתאימה. יש למקם חצים על המהלכים הראשוניים והאחרונים המציינים את כיוון הראייה יש למקם את החצים במרחק של 2...3 מ"מ מהקצה החיצוני של המהלך.
עבור חיתוך מורכב, משיכות קו החתך הפתוח מצוירות גם בכיפופי קו החתך.
ליד החצים המציינים את כיוון הראייה, אותיות גדולות של האלפבית הרוסי מוחלות בצד החיצוני של הפינה. ייעודי אותיות מוקצים בסדר אלפביתי ללא חזרות או השמטות.
את החתך עצמו יש לסמן בכיתוב כמו A-A
אם מישור החותך עולה בקנה אחד עם מישור הסימטריה של האובייקט, והחתך נעשה במיקום התצוגה המקבילה בחיבור ההקרנה, אז עבור קטעים אופקיים, חזיתיים ופרופילים אין צורך לסמן את מיקום הסקאנט. המטוס והחתך אינו מלווה בכתובת.
אם קו המתאר של אובייקט עולה בקנה אחד עם ציר הסימטריה, אז הגבול בין הנוף לקטע מסומן על ידי קו גלי, אשר מצויר כך שתמונת הקצה נשמרת.
