Svarbios pastabos!
1. Jei vietoj formulių matote gobbledygook, išvalykite talpyklą. Kaip tai padaryti savo naršyklėje, parašyta čia:
2. Prieš pradėdami skaityti straipsnį, atkreipkite dėmesį į mūsų navigatorių, kuriame rasite naudingiausių išteklių
1. Lygiagretainis
Sudėtinis žodis „lygiagretainė“? O už jos slypi labai paprasta figūra.
Na, tai yra, mes paėmėme dvi lygiagrečias linijas:

Perbraukė dar du:

O viduje yra lygiagretainis!
Kokias savybes turi lygiagretainis?
Lygiagretainio savybės.
Tai yra, ką galite naudoti, jei problemai pateikiamas lygiagretainis?
Į šį klausimą atsako ši teorema:
Nupieškime viską detaliai.
Ką tai reiškia pirmasis teoremos taškas? Ir faktas yra tas, kad jei TURITE lygiagretainį, tai tikrai turėsite
Antrasis taškas reiškia, kad jei yra lygiagretainis, tai vėlgi, tikrai:
Na, ir galiausiai, trečiasis taškas reiškia, kad jei TURITE lygiagretainį, būtinai:
Ar matote, koks didelis pasirinkimas? Ką naudoti sprendžiant problemą? Pabandykite sutelkti dėmesį į užduoties klausimą arba tiesiog išbandykite viską po vieną – tiks koks nors „raktas“.
Dabar užduokime sau kitą klausimą: kaip galime atpažinti lygiagretainį „iš žvilgsnio“? Kas turi nutikti keturkampiui, kad turėtume teisę suteikti jam lygiagretainio „pavadinimą“?
Į šį klausimą atsako keli lygiagretainio ženklai.
Lygiagretainio ženklai.
Dėmesio! Pradėkite.
Lygiagretainis.
Atkreipkite dėmesį: jei savo užduotyje radote bent vieną ženklą, tada tikrai turite lygiagretainį ir galite naudoti visas lygiagretainio savybes.
2. Stačiakampis
Manau, kad tai jums nebus naujiena
Pirmas klausimas: ar stačiakampis yra lygiagretainis?
Žinoma, kad yra! Juk jis turi – atsimeni, mūsų 3 ženklą?
Ir iš čia, žinoma, išplaukia, kad stačiakampyje, kaip ir bet kuriame lygiagrečiame, įstrižainės dalijamos per pusę susikirtimo taško.
Tačiau stačiakampis taip pat turi vieną išskirtinę savybę.
Stačiakampio savybė
Kodėl ši savybė yra išskirtinė? Nes joks kitas lygiagretainis neturi lygių įstrižainių. Suformuluokime tai aiškiau.
Atkreipkite dėmesį: norint tapti stačiakampiu, keturkampis pirmiausia turi tapti lygiagrečiu, o tada parodyti įstrižainių lygybę.
3. Deimantas
Ir vėl klausimas: ar rombas yra lygiagretainis, ar ne?
Su visa dešine - lygiagretainis, nes jis turi ir (prisiminkite mūsų 2 požymį).
Ir vėlgi, kadangi rombas yra lygiagretainis, tai jis turi turėti visas lygiagretainio savybes. Tai reiškia, kad rombe priešingi kampai yra lygūs, priešingos kraštinės lygiagrečios, o įstrižainės susikirtimo taške pasiskirsto per pusę.
Rombo savybės
Pažiūrėk į nuotrauką:

Kaip ir stačiakampio atveju, šios savybės yra skiriamosios, tai yra, dėl kiekvienos iš šių savybių galime daryti išvadą, kad tai ne tik lygiagretainis, o rombas.
Deimanto ženklai


Ir vėl atkreipkite dėmesį: turi būti ne tik keturkampis, kurio įstrižainės būtų statmenos, bet lygiagretainis. Įsitikinkite:
Ne, žinoma, nors jos įstrižainės yra statmenos, o įstrižainė yra kampų ir pusiausvyra. Bet... įstrižainės nedalomos per pusę susikirtimo taško, todėl - NE lygiagretainis, taigi NE rombas.
Tai yra, kvadratas yra stačiakampis ir rombas vienu metu. Pažiūrėkim, kas nutiks.
Ar aišku kodėl? - rombas yra kampo A pusiausvyra, kuri yra lygi. Tai reiškia, kad jis dalijasi (ir taip pat) į du kampus.
Na, tai visiškai aišku: stačiakampio įstrižainės yra lygios; Rombo įstrižainės yra statmenos, ir apskritai įstrižainių lygiagretainis yra padalintas per pusę iš susikirtimo taško.
VIDUTINIS LYGIS
Keturkampių savybės. Lygiagretainis

Lygiagretainio savybės
Dėmesio! Žodžiai" lygiagretainio savybės"Tai reiškia, kad jei jūsų užduotis Yra lygiagretainis, tada galima naudoti visus toliau nurodytus dalykus.
Lygiagretainio savybių teorema.
Bet kuriame lygiagrečiame:
Kitaip tariant, supraskime, kodėl visa tai tiesa Įrodysime teorema.
Taigi kodėl 1) yra tiesa?
Jei tai lygiagretainis, tada:
- guli kryžmai
- guli kaip kryžiai.
Tai reiškia (pagal II kriterijų: ir - bendras.)
Na, štai, štai! - įrodytas.
Bet beje! Mes taip pat įrodėme 2)!
Kodėl? Bet (pažiūrėkite į paveikslėlį), tai yra būtent todėl.
Liko tik 3).
Norėdami tai padaryti, vis tiek turite nubrėžti antrą įstrižainę.
Ir dabar tai matome - pagal II charakteristiką (kampai ir pusė „tarp jų“).
Savybės įrodytos! Pereikime prie ženklų.
Lygiagretainio ženklai
Prisiminkite, kad lygiagretainis ženklas atsako į klausimą „kaip tu žinai, kad figūra yra lygiagretainis?
Piktogramose tai atrodo taip:
Kodėl? Būtų malonu suprasti kodėl – užteks. Bet žiūrėk:
Na, mes supratome, kodėl 1 ženklas yra teisingas.
Na, tai dar lengviau! Vėl nubrėžkime įstrižainę.
Tai reiškia:
IR Taip pat lengva. Bet... kitaip!
Reiškia,. Oho! Bet taip pat - vidinis vienpusis su sekantu!
Todėl faktas tai reiškia.
O jei pažiūrėsi iš kitos pusės, tai – vidinis vienpusis su sekantu! Ir todėl.
Ar matai, kaip tai puiku?!
Ir vėl paprasta:
Lygiai taip pat.
Atkreipk dėmesį: jei rastum bent jau vienas lygiagretainio ženklas jūsų uždavinyje, tada jūs turite tiksliai lygiagretainis ir galite naudoti Visi lygiagretainio savybės.
Norėdami aiškumo, pažiūrėkite į diagramą:

Keturkampių savybės. Stačiakampis.
Stačiakampio savybės:
1) punktas gana akivaizdus – juk 3 () ženklas tiesiog įvykdytas
Ir 2 punktas - labai svarbus. Taigi, įrodykime tai
Tai reiškia iš dviejų pusių (ir – bendrai).
Na, o kadangi trikampiai yra lygūs, tai ir jų hipotenuzės yra lygios.
Tai įrodė!
Ir įsivaizduokite, kad įstrižainių lygybė yra išskirtinė stačiakampio savybė tarp visų lygiagrečių. Tai yra, šis teiginys yra teisingas^
Supraskime kodėl?
Tai reiškia (tai reiškia lygiagretainio kampus). Tačiau dar kartą prisiminkime, kad tai lygiagretainis, taigi.
Reiškia,. Na, žinoma, iš to išplaukia, kad kiekvienas iš jų! Juk jie turi duoti iš viso!
Taigi jie įrodė, kad jei lygiagretainis staiga (!) įstrižainės tampa lygios, tada tai tiksliai stačiakampis.
Bet! Atkreipk dėmesį! Tai yra apie lygiagretainiai! Ne bet kas lygių įstrižainių keturkampis yra stačiakampis ir tik lygiagretainis!
Keturkampių savybės. Rombas
Ir vėl klausimas: ar rombas yra lygiagretainis, ar ne?
Su visa dešine - lygiagretainis, nes jis turi (Prisiminkite mūsų 2 funkciją).
Ir vėlgi, kadangi rombas yra lygiagretainis, jis turi turėti visas lygiagretainio savybes. Tai reiškia, kad rombe priešingi kampai yra lygūs, priešingos kraštinės lygiagrečios, o įstrižainės susikirtimo taške pasiskirsto per pusę.
Tačiau yra ir ypatingų savybių. Suformuluokime.
Rombo savybės
Kodėl? Na, o kadangi rombas yra lygiagretainis, tai jo įstrižainės dalijamos pusiau.
Kodėl? Taip, štai kodėl!
Kitaip tariant, įstrižainės pasirodė esąs rombo kampų pusiausvyros.
Kaip ir stačiakampio atveju, šios savybės yra savitas, kiekvienas iš jų taip pat yra rombo ženklas.
Deimantų ženklai.
Kodėl tai? Ir žiūrėk,
Tai reiškia tiekŠie trikampiai yra lygiašoniai.
Kad būtų rombas, keturkampis pirmiausia turi „tapti“ lygiagretainiu, o tada parodyti 1 arba 2 požymį.
Keturkampių savybės. Kvadratas
Tai yra, kvadratas yra stačiakampis ir rombas vienu metu. Pažiūrėkim, kas nutiks.
Ar aišku kodėl? Kvadratas – rombas – yra kampo, kuris lygus, pusiausvyra. Tai reiškia, kad jis dalijasi (ir taip pat) į du kampus.
Na, tai visiškai aišku: stačiakampio įstrižainės yra lygios; Rombo įstrižainės yra statmenos, ir apskritai įstrižainių lygiagretainis yra padalintas per pusę iš susikirtimo taško.
Kodėl? Na, tiesiog pritaikykime Pitagoro teoremą...
SANTRAUKA IR PAGRINDINĖS FORMULĖS
Lygiagretainio savybės:
- Priešingos pusės yra lygios: , .
- Priešingi kampai yra lygūs: , .
- Kampai vienoje pusėje sudaro: , .
- Įstrižainės dalijamos per pusę susikirtimo taško: .
Stačiakampio savybės:
- Stačiakampio įstrižainės lygios: .
- Stačiakampis yra lygiagretainis (stačiakampiui įvykdytos visos lygiagretainio savybės).
Rombo savybės:
- Rombo įstrižainės yra statmenos: .
- Rombo įstrižainės yra jo kampų pusiausvyros: ; ; ; .
- Rombas yra lygiagretainis (rombui įvykdytos visos lygiagretainio savybės).
Kvadrato savybės:
Kvadratas yra rombas ir stačiakampis tuo pačiu metu, todėl kvadratui yra įvykdytos visos stačiakampio ir rombo savybės. Ir:
Na, tema baigta. Jei skaitote šias eilutes, tai reiškia, kad esate labai šaunus.
Nes tik 5% žmonių sugeba ką nors įvaldyti patys. Ir jei perskaitėte iki galo, tada esate šiame 5%!
Dabar svarbiausia.
Jūs supratote šios temos teoriją. Ir, kartoju, tai... tai tiesiog super! Jūs jau esate geresnis už didžiąją daugumą jūsų bendraamžių.
Problema ta, kad to gali nepakakti...
Kam?
Už sėkmingai išlaikiusį vieningą valstybinį egzaminą, už įstojimą į kolegiją neviršijant biudžeto ir, SVARBIAUSIA, visam gyvenimui.
Niekuo neįtikinsiu, pasakysiu tik vieną dalyką...
Žmonės, gavę gerą išsilavinimą, uždirba daug daugiau nei tie, kurie jo negavo. Tai yra statistika.
Tačiau tai nėra pagrindinis dalykas.
Svarbiausia, kad jie būtų LAIMINGESNI (yra tokių tyrimų). Galbūt todėl, kad prieš juos atsiveria daug daugiau galimybių ir gyvenimas tampa šviesesnis? nezinau...
Bet pagalvok pats...
Ko reikia, kad būtumėte tikri, kad vieningo valstybinio egzamino metu būtumėte geresni už kitus ir galiausiai būtumėte... laimingesni?
ĮGYKITE SAVO RANKĄ SPRĘSDAMI ŠIOS TEmos problemas.
Per egzaminą teorijos neprašys.
Jums reikės spręsti problemas prieš laiką.
Ir, jei jų neišsprendėte (DAUG!), tikrai kur nors padarysite kvailą klaidą arba tiesiog neturėsite laiko.
Tai kaip sporte – reikia kartoti daug kartų, kad laimėtum užtikrintai.
Raskite kolekciją, kur tik norite, būtinai su sprendimais, detalia analize ir nuspręsk, nuspręsk, nuspręsk!
Galite naudoti mūsų užduotis (neprivaloma) ir mes, žinoma, jas rekomenduojame.
Kad galėtumėte geriau atlikti užduotis, turite padėti pratęsti šiuo metu skaitomo YouClever vadovėlio gyvavimo laiką.
Kaip? Yra dvi parinktys:
- Atrakinkite visas paslėptas užduotis šiame straipsnyje -
- Atrakinkite prieigą prie visų paslėptų užduočių visuose 99 vadovėlio straipsniuose - Pirkite vadovėlį - 499 RUR
Taip, mūsų vadovėlyje yra 99 tokie straipsniai ir iš karto galima atidaryti visas užduotis ir visus paslėptus tekstus.
Prieiga prie visų paslėptų užduočių suteikiama VISĄ svetainės gyvenimą.
Apibendrinant...
Jei jums nepatinka mūsų užduotys, susiraskite kitus. Tiesiog nesustokite ties teorija.
„Supratau“ ir „aš galiu išspręsti“ yra visiškai skirtingi įgūdžiai. Jums reikia abiejų.
Raskite problemas ir jas spręskite!
Sprendžiant problemas šia tema, išskyrus pagrindinės savybės lygiagretainis ir atitinkamas formules, galite atsiminti ir taikyti:
- Lygiagretainio vidinio kampo bisektorius atkerta iš jo lygiašonį trikampį
- Vidinių kampų, esančių greta vienos iš lygiagretainio kraštinių, bisektoriai yra vienas kitą statmeni
- Bisektoriai, kylantys iš priešingų vidinių lygiagretainio kampų, yra lygiagrečiai vienas kitam arba yra toje pačioje tiesėje
- Lygiagretainio įstrižainių kvadratų suma lygi jo kraštinių kvadratų sumai
- Lygiagretainio plotas lygus pusei įstrižainių sandaugos ir kampo tarp jų sinuso
Panagrinėkime problemas, kuriose šios savybės naudojamos.
1 užduotis.
Lygiagretainio ABCD kampo C bisektorius kerta kraštinę AD taške M ir kraštinės AB tęsinį už taško A taške E. Raskite lygiagretainio perimetrą, jei AE = 4, DM = 3.
Sprendimas.
1. Trikampis CMD yra lygiašonis. (1 nuosavybė). Todėl CD = MD = 3 cm.
2. Trikampis EAM yra lygiašonis.
Todėl AE = AM = 4 cm.
3. AD = AM + MD = 7 cm.
4. Perimetras ABCD = 20 cm.
Atsakymas. 20 cm.
2 užduotis.
Išgaubtame keturkampyje ABCD brėžiamos įstrižainės. Yra žinoma, kad trikampių ABD, ACD, BCD plotai yra lygūs. Įrodykite, kad šis keturkampis yra lygiagretainis.

Sprendimas.
1. Tegu BE yra trikampio ABD aukštis, CF – trikampio ACD aukštis. Kadangi pagal uždavinio sąlygas trikampių plotai yra lygūs ir jie turi bendrą pagrindą AD, tai šių trikampių aukščiai yra vienodi. BE = CF.
2. BE, CF yra statmenos AD. Taškai B ir C yra toje pačioje pusėje tiesės AD atžvilgiu. BE = CF. Todėl tiesi linija BC || REKLAMA. (*)
3. Tegu AL yra trikampio ACD aukštis, BK – trikampio BCD aukštis. Kadangi pagal uždavinio sąlygas trikampių plotai yra lygūs ir jie turi bendrą pagrindą CD, tai šių trikampių aukščiai yra vienodi. AL = BK.
4. AL ir BK yra statmenos CD. Taškai B ir A yra toje pačioje pusėje tiesios linijos CD atžvilgiu. AL = BK. Todėl tiesė AB || CD (**)
5. Iš sąlygų (*), (**) išplaukia, kad ABCD yra lygiagretainis.
Atsakymas. Įrodyta. ABCD yra lygiagretainis.
3 užduotis.
Lygiagretainio ABCD kraštinėse BC ir CD atitinkamai pažymėti taškai M ir H, kad atkarpos BM ir HD susikirstų taške O;<ВМD = 95 о,
 Sprendimas.
Sprendimas.
1. Trikampyje DOM<МОD = 25 о (Он смежный с <ВОD = 155 о); <ОМD = 95 о. Тогда <ОDМ = 60 о.
2. Stačiame trikampyje DHC Tada<НСD = 30 о. СD: НD = 2: 1 Bet CD = AB. Tada AB: HD = 2:1. 3. <С = 30 о, 4. <А = <С = 30 о, <В = Atsakymas: AB: HD = 2:1,<А = <С = 30 о, <В = 4 užduotis. Viena iš 4√6 ilgio lygiagretainio įstrižainių sudaro 60° kampą su pagrindu, o antroji įstrižainė sudaro 45° kampą su tuo pačiu pagrindu. Raskite antrąją įstrižainę. Sprendimas.
1. AO = 2√6. 2. Trikampiui AOD pritaikome sinuso teoremą. AO/sin D = OD/sin A. 2√6/sin 45 o = OD/sin 60 o. ОD = (2√6sin 60 о) / sin 45 о = (2√6 · √3/2) / (√2/2) = 2√18/√2 = 6. Atsakymas: 12.
5 užduotis. Lygiagretainio, kurio kraštinės yra 5√2 ir 7√2, mažesnis kampas tarp įstrižainių yra lygus mažesniam lygiagretainio kampui. Raskite įstrižainių ilgių sumą. Sprendimas.
Tegu lygiagretainio įstrižainės yra d 1, d 2, o kampas tarp įstrižainių ir mažesniojo lygiagretainio kampo lygus φ. 1. Suskaičiuokime du skirtingus S ABCD = AB AD sin A = 5√2 7√2 sin f, S ABCD = 1/2 AC ВD sin AOB = 1/2 d 1 d 2 sin f. Gauname lygybę 5√2 · 7√2 · sin f = 1/2d 1 d 2 sin f arba 2 · 5√2 · 7√2 = d 1 d 2; 2. Naudodamiesi lygiagretainio kraštinių ir įstrižainių ryšiu, užrašome lygybę (AB 2 + AD 2) 2 = AC 2 + BD 2. ((5√2) 2 + (7√2) 2) 2 = d 1 2 + d 2 2. d 1 2 + d 2 2 = 296. 3. Sukurkime sistemą: (d 1 2 + d 2 2 = 296, Padauginkime antrąją sistemos lygtį iš 2 ir pridėkime prie pirmosios. Gauname (d 1 + d 2) 2 = 576. Taigi Id 1 + d 2 I = 24. Kadangi d 1, d 2 yra lygiagretainio įstrižainių ilgiai, tai d 1 + d 2 = 24. Atsakymas: 24.
6 užduotis. Lygiagretainio kraštinės yra 4 ir 6. Smailusis kampas tarp įstrižainių yra 45 laipsniai. Raskite lygiagretainio plotą. Sprendimas.
1. Iš trikampio AOB, naudodamiesi kosinuso teorema, užrašome ryšį tarp lygiagretainio kraštinės ir įstrižainių. AB 2 = AO 2 + VO 2 2 · AO · VO · cos AOB. 4 2 = (d 1 / 2) 2 + (d 2 / 2) 2 - 2 · (d 1/2) · (d 2 / 2) cos 45 o; d 1 2/4 + d 2 2/4 – 2 · (d 1/2) · (d 2/2)√2/2 = 16. d 1 2 + d 2 2 – d 1 · d 2 √2 = 64. 2. Panašiai rašome santykį trikampiui AOD. Atsižvelgkime į tai<АОD = 135 о и cos 135 о = -cos 45 о = -√2/2. Gauname lygtį d 1 2 + d 2 2 + d 1 · d 2 √2 = 144. 3. Mes turime sistemą Iš antrosios lygties atėmę pirmąją, gauname 2d 1 · d 2 √2 = 80 arba d 1 d 2 = 80/(2√2) = 20√2 4. S ABCD = 1/2 AC ВD sin AOB = 1/2 d 1 d 2 sin α = 1/2 20√2 √2/2 = 10. Pastaba:Šioje ir ankstesnėje užduotyje nereikia visiškai išspręsti sistemos, numatant, kad šioje užduotyje plotui apskaičiuoti reikia įstrižainių sandaugos. Atsakymas: 10. 7 užduotis. Lygiagretainio plotas yra 96, o jo kraštinės yra 8 ir 15. Raskite mažesnės įstrižainės kvadratą. Sprendimas.
1. S ABCD = AB · AD · sin ВAD. Pakeiskime formulę. Gauname 96 = 8 · 15 · sin ВAD. Taigi nuodėmė ВAD = 4/5. 2. Raskime cos VAD. sin 2 VAD + cos 2 VAD = 1. (4 / 5) 2 + cos 2 VAD = 1. cos 2 VAD = 9 / 25. Pagal uždavinio sąlygas randame mažesnės įstrižainės ilgį. Įstrižainė ВD bus mažesnė, jei kampas ВАD yra smailus. Tada cos VAD = 3/5. 3. Iš trikampio ABD, pasitelkę kosinuso teoremą, randame įstrižainės BD kvadratą. ВD 2 = АВ 2 + АD 2 – 2 · АВ · ВD · cos ВAD. ВD 2 = 8 2 + 15 2 – 2 8 15 3 / 5 = 145. Atsakymas: 145.
Vis dar turite klausimų? Nežinote, kaip išspręsti geometrijos problemą? svetainėje, kopijuojant visą medžiagą ar jos dalį, būtina nuoroda į šaltinį. Lygiagretainis yra keturkampis, kurio priešingos kraštinės lygiagrečios, t.y. gulėti ant lygiagrečių linijų Lygiagretainio savybės: Lygiagretainio ženklai Geometrijoje nagrinėjami ypatingi lygiagretainių atvejai. Pamokos santrauka. Algebra 8 klasė Mokytojas Sysoy A.K. Mokykla 1828 m Pamokos tema: „Paralelograma ir jos savybės“ Pamokos tipas: kombinuotas
Pamokos tikslai:
1) Užtikrinti naujos sąvokos – lygiagretainio ir jo savybių įsisavinimą 2) Toliau ugdyti įgūdžius ir gebėjimus spręsti geometrines problemas; 3) Matematinio kalbėjimo kultūros ugdymas Pamokos planas:
1. Organizacinis momentas
(1 skaidrė) Skaidrėje rodomas Lewiso Carrollo pareiškimas. Mokiniai informuojami apie pamokos tikslą. Tikrinamas mokinių pasirengimas pamokai. 2. Žinių atnaujinimas
(2 skaidrė) Lentoje yra žodinio darbo užduotys. Mokytojas kviečia mokinius susimąstyti apie šias problemas ir pakelti rankas tiems, kurie supranta, kaip išspręsti problemą. Išsprendęs du uždavinius, prie lentos kampų sumos teoremai įrodyti kviečiamas studentas, kuris savarankiškai padaro papildomas konstrukcijas brėžinyje ir įrodo teoremą žodžiu. Studentai naudoja daugiakampio kampų sumos formulę: 3. Pagrindinė dalis
(3 skaidrė) Lygiagretainio apibrėžimas lentoje. Mokytojas pasakoja apie naują figūrą ir suformuluoja apibrėžimą, atlikdamas reikiamus paaiškinimus, naudodamas piešinį. Tada languotoje pristatymo dalyje, naudodamas žymeklį ir liniuotę, jis parodo, kaip nubrėžti lygiagretainį (galimi keli atvejai) (4 skaidrė) Mokytojas suformuluoja pirmąją lygiagretainio savybę. Kviečia mokinius iš piešinio pasakoti, kas duota ir ką reikia įrodyti. Po to pateikta užduotis pasirodo lentoje. Mokiniai spėja (gal ir mokytojo pagalba), kad reikiamos lygybės turi būti įrodytos per trikampių lygybes, kurias galima gauti nubrėžus įstrižainę (lentoje atsiranda įstrižainė). Toliau mokiniai atspėja, kodėl trikampiai yra lygūs, ir įvardija ženklą, kad trikampiai lygūs (atsiranda atitinkama forma). Jie žodžiu perduoda faktus, kurių reikia, kad trikampiai būtų lygūs (kaip jie juos įvardija, atsiranda atitinkama vizualizacija). Toliau studentai suformuluoja sutampančių trikampių savybę, kuri pasirodo kaip 3 įrodymo taškas, ir tada savarankiškai užbaigia teoremos įrodymą žodžiu. (5 skaidrė) Mokytojas suformuluoja antrąją lygiagretainio savybę. Lentoje pasirodo lygiagretainio brėžinys. Mokytojas siūlo paveikslėliu pasakyti, kas duota ir ką reikia įrodyti. Mokiniams teisingai pranešus, kas duota ir ką reikia įrodyti, atsiranda teoremos sąlyga. Mokiniai spėja, kad įstrižainių dalių lygybę galima įrodyti trikampių lygybeAOB Ir MENKĖ.. Naudojant ankstesnę lygiagretainio savybę, spėjama, kad kraštinės yra lygiosAB Ir CD. Tada jie supranta, kad reikia rasti vienodus kampus ir, naudodamiesi lygiagrečių tiesių savybėmis, įrodyti kampų, besiribojančių su lygiomis kraštinėmis, lygybę. Šie etapai vaizduojami skaidrėje. Teoremos teisingumas išplaukia iš trikampių lygybės – mokiniai tai pasako ir skaidrėje atsiranda atitinkama vizualizacija. (6 skaidrė) Mokytojas suformuluoja trečiąją lygiagretainio savybę. Atsižvelgdamas į tai, kiek liko iki pamokos pabaigos, mokytojas gali suteikti galimybę mokiniams patiems įrodyti šią savybę arba apsiriboti jos formulavimu, o patį įrodinėjimą palikti mokiniams kaip namų darbus. Įrodymas gali būti pagrįstas įbrėžto daugiakampio kampų suma, kuri buvo pakartota pamokos pradžioje, arba dviejų lygiagrečių tiesių vidinių vienpusių kampų sumaREKLAMA Ir B.C., ir, pavyzdžiui, sekantąAB.
4. Medžiagos tvirtinimas
Šiame etape mokiniai problemoms spręsti naudoja anksčiau išmoktas teoremas. Studentai pasirenka idėjas, kaip savarankiškai spręsti problemą. Kadangi galimų projektavimo variantų yra daug ir jie visi priklauso nuo to, kaip mokiniai ieškos problemos sprendimo, problemų sprendimo vizualizacija nėra, o kiekvieną sprendimo etapą studentai patys braižo ant atskiros lentos. su sprendimo įrašymu į sąsiuvinį. (7 skaidrė) Pasirodo užduoties sąlyga. Mokytojas siūlo formuluoti „Duota“ pagal sąlygą. Mokiniams teisingai užrašius trumpą sąlygos teiginį, lentoje pasirodo „Duota“. Problemos sprendimo procesas gali atrodyti taip: Nubrėžkime aukštį BH (vizualizuotas) Trikampis AHB yra stačiakampis. Kampas A lygus kampui C ir lygus 30 0 (pagal lygiagretainio priešingų kampų savybę). 2BH =AB (pagal kojos, esančios priešais 30 0 kampą stačiakampiame trikampyje, savybę). Taigi AB = 13 cm. AB = CD, BC = AD (pagal lygiagretainio priešingų kraštinių savybę) Taigi AB = CD = 13 cm. Kadangi lygiagretainio perimetras yra 50 cm, tai BC = AD = (50 – 26): 2 = 12 cm. Atsakymas: AB = CD = 13 cm, BC = AD = 12 cm. (8 skaidrė) Pasirodo užduoties sąlyga. Mokytojas siūlo formuluoti „Duota“ pagal sąlygą. Tada ekrane pasirodo „Given“. Naudojant raudonas linijas, paryškinamas keturkampis, apie kurį reikia įrodyti, kad tai lygiagretainis. Problemos sprendimo procesas gali atrodyti taip: Nes BK ir MD yra statmenos vienai tiesei, tada tiesės BK ir MD yra lygiagrečios. Per gretimus kampus galima parodyti, kad tiesių BM ir KD vidinių vienpusių kampų ir atkarpos MD suma lygi 180 0. Todėl šios linijos yra lygiagrečios. Kadangi keturkampio BMDK priešingos pusės yra lygiagrečios poromis, tai šis keturkampis yra lygiagretainis. 5. Pamokos pabaiga. Rezultatų elgsena.
(8 skaidrė) Skaidrėje atsiranda klausimai nauja tema, į kuriuos mokiniai atsako.
(
(Kadangi stačiakampiame trikampyje koja, esanti priešais 30° kampą, yra lygi pusei hipotenuzės).
 būdais jo plotas.
būdais jo plotas.
(d 1 + d 2 = 140.
(d 1 2 + d 2 2 – d 1 · d 2 √2 = 64,
(d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
Norėdami gauti pagalbos iš dėstytojo, užsiregistruokite.
Pirma pamoka nemokama!
 22 teorema.
Lygiagretainio priešingos kraštinės yra lygios.
22 teorema.
Lygiagretainio priešingos kraštinės yra lygios.
Įrodymas. Lygiagretainyje ABCD nubrėžiame įstrižainę AC. Trikampiai ACD ir ACB yra sutampa, nes turi bendrą kraštinę AC ir dvi lygių kampų poras. greta jo: ∠ CAB=∠ ACD, ∠ ACB=∠ DAC (kaip skersiniai kampai su lygiagrečiomis tiesėmis AD ir BC). Tai reiškia, kad AB = CD ir BC = AD, kaip atitinkamos lygių trikampių kraštinės ir kt. Iš šių trikampių lygybės taip pat išplaukia, kad atitinkami trikampių kampai yra lygūs:
23 teorema.
Lygiagretainio priešingi kampai yra lygūs: ∠ A=∠ C ir ∠ B=∠ D.
Pirmosios poros lygybė gaunama iš trikampių ABD ir CBD lygybės, o antrosios - ABC ir ACD.
24 teorema.
Gretimi lygiagretainio kampai, t.y. kampai, esantys šalia vienos pusės, sudaro 180 laipsnių.
Taip yra todėl, kad jie yra vidiniai vienpusiai kampai.
25 teorema.
Lygiagretainio įstrižainės viena kitą dalija susikirtimo taške.
Įrodymas. Apsvarstykite trikampius BOC ir AOD. Pagal pirmąją savybę, AD=BC ∠ OAD=∠ OCB ir ∠ ODA=∠ OBC yra kryžminės lygiagrečios tiesės AD ir BC. Todėl trikampiai BOC ir AOD yra lygūs šoniniuose ir gretimuose kampuose. Tai reiškia, kad BO = OD ir AO = OS, kaip ir atitinkamos lygių trikampių kraštinės ir kt.
26 teorema.
Jei keturkampio priešingos kraštinės yra lygios poromis, tai yra lygiagretainis.
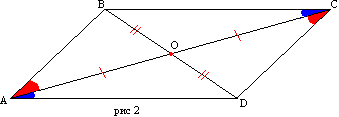
Įrodymas. Tegu keturkampio ABCD kraštinės AD ir BC, AB ir CD atitinkamai lygios (2 pav.). Nubrėžkime įstrižainę AC. Trikampiai ABC ir ACD yra lygūs iš trijų kraštinių. Tada kampai BAC ir DCA yra lygūs, todėl AB lygiagreti CD. Kraštinių BC ir AD lygiagretumas išplaukia iš kampų CAD ir ACB lygybės.
27 teorema.
Jei keturkampio priešingi kampai poromis lygūs, tai lygiagretainis.
Tegu ∠ A=∠ C ir ∠ B=∠ D. Kadangi ∠ A+∠ B+∠ C+∠ D=360 o, tada ∠ A+∠ B=180 o ir kraštinės AD ir BC lygiagrečios (remiantis tiesių lygiagretumu). Taip pat įrodysime kraštinių AB ir CD lygiagretumą ir padarysime išvadą, kad ABCD pagal apibrėžimą yra lygiagretainis.
28 teorema.
Jeigu gretimi keturkampio kampai, t.y. Kampai, esantys greta vienos pusės, sudaro 180 laipsnių, tada tai yra lygiagretainis.
Jei vidiniai vienpusiai kampai sudaro 180 laipsnių, tiesios linijos yra lygiagrečios. Taigi AB lygiagreti CD, o BC lygiagreti AD. Keturkampis pagal apibrėžimą pasirodo esąs lygiagretainis.
29 teorema.
Jei keturkampio įstrižainės susikirtimo taške dalija viena kitą, tai keturkampis yra lygiagretainis.
Įrodymas. Jei AO = OC, BO = OD, tai trikampiai AOD ir BOC yra lygūs, kaip turintys lygius (vertikalius) kampus viršūnėje O, uždarytus tarp lygių kraštinių porų. Iš trikampių lygybės darome išvadą, kad AD ir BC yra lygūs. Kraštinės AB ir CD taip pat yra lygios, o keturkampis pagal 1 kriterijų pasirodo lygiagretainiu.
30 teorema.
Jei keturkampis turi porą lygiagrečių lygiagrečių kraštinių, tai jis yra lygiagretainis.
Tegul keturkampio ABCD kraštinės AB ir CD yra lygiagrečios ir lygios. Nubrėžkime įstrižaines AC ir BD. Iš šių tiesių lygiagretumo matyti, kad skersiniai kampai ABO = CDO ir BAO = OCD yra lygūs. Trikampiai ABO ir CDO yra lygūs šoniniuose ir gretimuose kampuose. Todėl AO=OS, VO=ОD, t.y. Įstrižainės dalijamos per pusę susikirtimo taško, o keturkampis pagal 4 kriterijų pasirodo lygiagretainiu.







