Lezione sul tema “Prova di perpendicolarità di due piani”
L'idea di un piano nello spazio ci permette di ottenere, ad esempio, la superficie di un tavolo o di una parete. Tuttavia, un tavolo o un muro hanno dimensioni finite e il piano si estende oltre i suoi confini fino all'infinito.Consideriamo due piani che si intersecano. Quando si intersecano, formano quattro angoli diedri con un bordo comune.
Ricordiamo cos'è un angolo diedro.
In realtà incontriamo oggetti che hanno la forma di un angolo diedro: ad esempio una porta leggermente aperta o una cartella semiaperta.

Quando due piani alfa e beta si intersecano, otteniamo quattro angoli diedri. Sia uno degli angoli diedro uguale a (phi), allora il secondo è uguale a (180 0 –), terzo, quarto (180 0 -).

α Eβ, 0°< 90 °
Consideriamo il caso in cui uno degli angoli diedro è 90 0 .
Quindi, tutti gli angoli diedri in questo caso sono uguali a 90 0 .
angolo diedro tra i pianiα Eβ,
90º
Introduciamo la definizione di piani perpendicolari:
Due piani si dicono perpendicolari se l'angolo diedro che li separa è di 90°.
L'angolo tra i piani sigma ed epsilon è di 90 gradi, il che significa che i piani sono perpendicolari
Perché =90°
Diamo esempi di piani perpendicolari.
Parete e soffitto.
Parete laterale e piano del tavolo.

Parete e soffitto
Formuliamo un segno di perpendicolarità di due piani:
TEOREMA:Se uno dei due piani passa per una linea perpendicolare all'altro piano, allora questi piani sono perpendicolari.
Dimostriamo questo segno.
Per condizione si sa che la linea rettaAM giace nel piano α, la retta AM è perpendicolare al piano β,
Dimostrare: i piani α e β sono perpendicolari.
Prova:
1) Piani α eβ si intersecano lungo la retta AR, e AM AR, poiché AM β per condizione, cioè AM è perpendicolare a qualsiasi retta giacente nel piano β.
2) Tracciamo una retta nel piano βUNT perpendicolareUNR.
Otteniamo l'angolo TUNM è l'angolo lineare dell'angolo diedro. Ma l'angolo TUNM = 90°, poiché MA è β. Quindi αβ.
Q.E.D.
TEOREMA:Se un piano passa per una linea perpendicolare ad un altro piano, questi piani sono perpendicolari.

Dato:α, β, AM α, AMβ, AM∩=A
Dimostrare: αβ.
Prova:
1)α∩β = AR, mentre AM AR, poiché AM β per condizione, cioè AM è perpendicolare a qualsiasi retta giacente nel piano β.
2) ATβ,UNTUNR.
TAM è l'angolo lineare dell'angolo diedro. TAM = 90°, perché MAβ. Quindi αβ.
Q.E.D
Dal segno di perpendicolarità di due piani abbiamo un importante corollario:
IMPATTO:Un piano perpendicolare ad una linea lungo la quale due piani si intersecano è perpendicolare a ciascuno di questi piani.
Dimostriamo questo corollario: se il piano gamma è perpendicolare alla linea c, allora, in base al parallelismo dei due piani, gamma è perpendicolare ad alfa. Allo stesso modo, la gamma è perpendicolare alla beta

Cioè: se α∩β=с e γс, allora γα e γβ.
Perchéγс e сα dal segno di perpendicolarità γα.
Simile a γβ
Riformuliamo questo corollario per un angolo diedro:
Il piano passante per l'angolo lineare di un angolo diedro è perpendicolare allo spigolo e alle facce di questo angolo diedro. In altre parole, se abbiamo costruito un angolo lineare di un angolo diedro, allora il piano che lo attraversa è perpendicolare al bordo e alle facce di questo angolo diedro.

Compito.
Dato: ΔАВС, С = 90°, АС giace nel piano α, l'angolo tra i piani α eABC= 60°, AC = 5 cm, AB = 13 cm.
Trova: la distanza dal punto B al piano α.
Soluzione:
1) Costruiamo VC α. Allora KS è la proiezione del sole su questo piano.
2) BC AC (per condizione), che significa, secondo il teorema delle tre perpendicolari (TPP), KS AC. Pertanto, VSK è l'angolo lineare dell'angolo diedro tra il piano α e il piano del triangolo ABC. Cioè VSK = 60°.
3) Da ΔBCA secondo il teorema di Pitagora:
Da ΔVKS: ![]()
Questa lezione aiuterà coloro che desiderano comprendere l'argomento "Il segno di perpendicolarità di due piani". All'inizio ripeteremo la definizione di angoli diedri e lineari. Considereremo poi quali piani sono detti perpendicolari e dimostreremo il segno di perpendicolarità di due piani.
Argomento: Perpendicolarità di rette e piani
Lezione: Segno di perpendicolarità di due piani
Definizione. Un angolo diedro è una figura formata da due semipiani che non appartengono allo stesso piano e dalla loro retta comune a (a è uno spigolo).
Riso. 1
Consideriamo due semipiani α e β (Fig. 1). Il loro confine comune è l. Questa figura è chiamata angolo diedro. Due piani che si intersecano formano quattro angoli diedri con uno spigolo comune.
Un angolo diedro è misurato dal suo angolo lineare. Scegliamo un punto arbitrario sul bordo comune l dell'angolo diedro. Nei semipiani α e β, da questo punto tracciamo le perpendicolari a e b alla retta l e otteniamo l'angolo lineare dell'angolo diedro.
Le rette aeb formano quattro angoli uguali a φ, 180° - φ, φ, 180° - φ. Ricordiamo che l'angolo tra le rette è il più piccolo di questi angoli.
Definizione. L'angolo tra i piani è il più piccolo degli angoli diedri formati da questi piani. φ è l'angolo tra i piani α e β, se
Definizione. Due piani che si intersecano si dicono perpendicolari (mutuamente perpendicolari) se l'angolo tra loro è di 90°.

Riso. 2
Un punto arbitrario M viene selezionato sul bordo l (Fig. 2). Tracciamo due rette perpendicolari MA = a e MB = b allo spigolo l rispettivamente nel piano α e nel piano β. Abbiamo ottenuto l'angolo AMB. L'angolo AMB è l'angolo lineare di un angolo diedro. Se l'angolo AMB è 90° i piani α e β si dicono perpendicolari.
La linea b è perpendicolare alla linea l per costruzione. La linea b è perpendicolare alla linea a, poiché l'angolo tra i piani α e β è 90°. Troviamo che la linea b è perpendicolare a due linee che si intersecano a e l dal piano α. Ciò significa che la retta b è perpendicolare al piano α.
Allo stesso modo possiamo dimostrare che la retta a è perpendicolare al piano β. La linea a è perpendicolare alla linea l per costruzione. La linea a è perpendicolare alla linea b, poiché l'angolo tra i piani α e β è 90°. Troviamo che la linea a è perpendicolare a due linee intersecanti b e l dal piano β. Ciò significa che la retta a è perpendicolare al piano β.
Se uno dei due piani passa per una linea perpendicolare all'altro piano, allora tali piani sono perpendicolari.
Dimostrare:

Riso. 3
Prova:
Lasciamo che i piani α e β si intersechino lungo la retta AC (Fig. 3). Per dimostrare che i piani sono tra loro perpendicolari, devi costruire tra loro un angolo lineare e dimostrare che questo angolo è 90°.
La retta AB è perpendicolare al piano β, e quindi alla retta AC giacente nel piano β.
Disegniamo una linea retta AD perpendicolare ad una linea retta AC nel piano β. Allora BAD è l'angolo lineare dell'angolo diedro.
La retta AB è perpendicolare al piano β, e quindi alla retta AD giacente nel piano β. Ciò significa che l'angolo lineare BAD è 90°. Ciò significa che i piani α e β sono perpendicolari, che è ciò che doveva essere dimostrato.
Il piano perpendicolare alla linea lungo la quale si intersecano due piani dati è perpendicolare a ciascuno di questi piani (Fig. 4).
Dimostrare:

Riso. 4
Prova:
La retta l è perpendicolare al piano γ, e il piano α passa per la retta l. Ciò significa che secondo la perpendicolarità dei piani, i piani α e γ sono perpendicolari.
La retta l è perpendicolare al piano γ, e il piano β passa per la retta l. Ciò significa che secondo la perpendicolarità dei piani, i piani β e γ sono perpendicolari.
Definizione. Un angolo diedro è una figura formata da una retta a e da due semipiani aventi un confine comune a e non appartenenti allo stesso piano.
Definizione. La misura in gradi di un angolo diedro è la misura in gradi di uno qualsiasi dei suoi angoli lineari.
Definizione. Due piani che si intersecano si dicono perpendicolari se l'angolo formato da essi è di 90°.
Un segno di perpendicolarità di due piani.
Proprietà.
- In un cuboide, tutte e sei le facce sono rettangoli.
- Tutti gli angoli diedri di un cuboide sono retti
- Il quadrato della diagonale di un parallelepipedo rettangolo è uguale alla somma dei quadrati delle sue tre dimensioni.
Problemi e test sull'argomento "Argomento 7. "Angolo diedro. Perpendicolarità dei piani."
- Angolo diedro. Perpendicolarità dei piani
- Perpendicolarità di una retta e di un piano - Perpendicolarità di linee e piani, voto 10
Lezioni: 1 Compiti: 10 Test: 1
- Perpendicolare e obliquo. Angolo formato da una retta e da un piano - Perpendicolarità di linee e piani, voto 10
Lezioni: 2 Compiti: 10 Test: 1
- Parallelismo dei piani - Parallelismo di rette e piani, voto 10
Lezioni: 1 Compiti: 8 Test: 1
- Linee perpendicolari - Informazioni geometriche di base 7a elementare
Lezioni: 1 Compiti: 17 Test: 1
Il materiale sull'argomento riassume e sistematizza le informazioni che conosci dalla planimetria sulla perpendicolarità delle linee rette. Si consiglia di combinare lo studio dei teoremi sul rapporto tra parallelismo e perpendicolarità delle rette e dei piani nello spazio, nonché del materiale sulla perpendicolare e inclinato, con una ripetizione sistematica del materiale corrispondente dalla planimetria.
Le soluzioni di quasi tutti i problemi di calcolo si riducono all'applicazione del teorema di Pitagora e alle sue conseguenze. In molti problemi la possibilità di utilizzare il teorema di Pitagora o i suoi corollari è giustificata dal teorema delle tre perpendicolari o dalle proprietà di parallelismo e perpendicolarità dei piani.
Il concetto di piani perpendicolari
Quando due piani si intersecano, otteniamo angoli diedri $4$. Due angoli sono uguali a $\varphi $ e gli altri due sono uguali a $(180)^0-\varphi $.
Definizione 1
L'angolo tra i piani è il minimo degli angoli diedri formati da questi piani.
Definizione 2
Due piani che si intersecano sono detti perpendicolari se l'angolo tra questi piani è $90^\circ$ (Fig. 1).
Figura 1. Piani perpendicolari
Segno di perpendicolarità di due piani
Teorema 1
Se una retta di un piano è perpendicolare ad un altro piano, allora questi piani sono perpendicolari tra loro.
Prova.
Siano dati i piani $\alpha $ e $\beta $, che si intersecano lungo la retta $AC$. Sia la retta $AB$ giacente nel piano $\alpha $ perpendicolare al piano $\beta $ (Fig. 2).

Figura 2.
Poiché la linea $AB$ è perpendicolare al piano $\beta$, è anche perpendicolare alla linea $AC$. Tracciamo inoltre una linea $AD$ nel piano $\beta$, perpendicolare alla linea $AC$.
Troviamo che l'angolo $BAD$ è l'angolo lineare dell'angolo diedro, pari a $90^\circ$. Cioè, per la definizione 1, l'angolo tra i piani è $90^\circ$, il che significa che questi piani sono perpendicolari.
Il teorema è stato dimostrato.
Da questo teorema segue il seguente teorema.
Teorema 2
Se un piano è perpendicolare alla retta lungo la quale si intersecano altri due piani, allora è perpendicolare anche a questi piani.
Prova.
Siano dati due piani $\alpha $ e $\beta $ che si intersecano lungo la retta $c$. Il piano $\gamma $ è perpendicolare alla retta $c$ (Fig. 3)

Figura 3.
Poiché la linea $c$ appartiene al piano $\alpha $ e il piano $\gamma $ è perpendicolare alla linea $c$, allora, per il Teorema 1, i piani $\alpha $ e $\gamma $ sono perpendicolari.
Poiché la linea $c$ appartiene al piano $\beta $ e il piano $\gamma $ è perpendicolare alla linea $c$, allora, per il Teorema 1, i piani $\beta $ e $\gamma $ sono perpendicolari.
Il teorema è stato dimostrato.
Per ciascuno di questi teoremi è vera anche l’affermazione inversa.
Problemi di esempio
Esempio 1
Sia dato un parallelepipedo rettangolare $ABCDA_1B_1C_1D_1$. Trova tutte le coppie di piani perpendicolari (Fig. 5).

Figura 4.
Soluzione.
Per definizione di parallelepipedo rettangolare e piani perpendicolari, vediamo le seguenti otto coppie di piani perpendicolari tra loro: $(ABB_1)$ e $(ADD_1)$, $(ABB_1)$ e $(A_1B_1C_1)$, $( ABB_1)$ e $(BCC_1) $, $(ABB_1)$ e $(ABC)$, $(DCC_1)$ e $(ADD_1)$, $(DCC_1)$ e $(A_1B_1C_1)$, $(DCC_1) $ e $(BCC_1)$, $(DCC_1)$ e $(ABC)$.
Esempio 2
Siano dati due piani reciprocamente perpendicolari. Da un punto di un piano si traccia una perpendicolare ad un altro piano. Dimostrare che questa retta giace nel piano dato.
Prova.
Dati i piani perpendicolari $\alpha $ e $\beta $ che si intersecano lungo la retta $c$. Dal punto $A$ del piano $\beta $ si traccia una perpendicolare $AC$ al piano $\alpha $. Supponiamo che $AC$ non giaccia nel piano $\beta$ (Fig. 6).
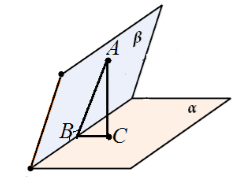
Figura 5.
Consideriamo il triangolo $ABC$. È rettangolare con angolo retto $ACB$. Pertanto $\angolo ABC\ne (90)^0$.
Ma d'altra parte $\angolo ABC$ è l'angolo lineare dell'angolo diedro formato da questi piani. Cioè, l'angolo diedro formato da questi piani non è uguale a 90 gradi. Troviamo che l'angolo tra i piani non è uguale a $90^\circ$. Contraddizione. Pertanto $AC$ si trova nel piano $\beta$.
Costruzione di due piani reciprocamente perpendicolari. Come è noto, i piani sono perpendicolari se una linea appartenente ad un piano è perpendicolare ad un altro piano. Pertanto un piano perpendicolare a un dato piano può essere tracciato attraverso una linea perpendicolare a un dato piano, oppure perpendicolare a una linea giacente in un dato piano.
Mostrato nella fig. 4.12 i piani (piano del triangolo ABC e piano P) sono tra loro perpendicolari, poiché il piano P è perpendicolare alla retta A1 giacente nel piano del triangolo. La proiezione del piano P passante per la linea con le proiezioni m 2 n 2, m 1 n 1 e perpendicolare al piano specificato dalle proiezioni a 2 b 2 c 2, a 1 b 1 c 1 del triangolo è mostrata in Fico. 4.12.
Costruzione: 1. Disegna le linee principali del piano, C1 - orizzontale, C2 - frontale.
2. Attraverso un punto arbitrario E (situato all'esterno del triangolo ABC), tracciare una linea retta EF perpendicolare alle linee principali del piano (c 2 f 2 è perpendicolare a c 2 2 2 e c 1 f 1 è perpendicolare a 1 1 1).
3. Attraverso il punto N, tracciamo una linea retta arbitraria EM intersecante con EF, otteniamo un piano P definito da due rette intersecanti (EM X EF).
Pertanto, il piano P(ME X EF) è perpendicolare al piano Q(triangolo ABC).
Va notato che per i piani tra loro perpendicolari in posizione generale, le loro tracce omonime non sono mai perpendicolari. Ma se uno dei piani dati (o entrambi) è un piano generale, allora la perpendicolarità reciproca sul diagramma di una coppia delle loro tracce indica la perpendicolarità dei piani nello spazio.
18) La retta d'intersezione di due piani può essere determinata dai loro due punti comuni. Per fare ciò, determinare i punti di intersezione di due rette qualsiasi di un piano con un altro piano o i punti di intersezione di una linea retta su ciascuno dei piani con un altro piano
Sequenza di costruzione:
La linea di intersezione di due piani può essere trovata utilizzando piani di taglio ausiliari durante la risoluzione. Solitamente vengono scelti i piani di proiezione (spesso orizzontali o frontali)
Selezionare un piano orizzontale ausiliario secante arbitrario Ф1; esso interseca i piani dati lungo le linee rette (12 e 34) che (su p1 si intersecano nel punto k)
Il secondo piano orizzontale secante interseca i piani dati anche lungo le orizzontali; questi, a loro volta, si intersecano nel punto E
La retta KE è la linea di intersezione dei piani dati.
Consideriamo la soluzione a questo problema su un disegno piatto.
1a fase della soluzione Per costruire il punto M, viene utilizzato un piano che si proietta orizzontalmente, il mediatore ("), che racchiude il lato AB del triangolo ABC.
2a fase della soluzione Costruiamo la linea di intersezione (nel disegno è specificata dai punti 1 e 2) del piano intermedio (") e il piano DEK.
3a fase della soluzione Trova il punto M di intersezione della linea 1 - 2 con la linea AB.
È stato trovato un punto M della linea di intersezione desiderata.
Per costruire il punto N, viene utilizzato un piano proiettante orizzontalmente ("), che racchiude il lato AC del triangolo ABC.
Le costruzioni sono simili alle precedenti.
La determinazione della visibilità sul piano H viene effettuata utilizzando i punti 4 e 8 concorrenti orizzontalmente
Il punto 4 si trova sopra il punto 8 (4" e 8"), quindi sul piano H la parte del triangolo DEK, situata verso il punto 4, copre la parte del triangolo ABC, situata dalla linea di intersezione verso il punto 8. Con l'aiuto di viene determinata una coppia di punti 6 e 7 in competizione frontale visibilità sul piano V.

Intersezione di due piani sporgenti frontalmente (?)
L'intersezione di due piani sporgenti orizzontalmente (?)
19) Un taglio è un'immagine di un oggetto sezionato mentalmente da uno o più piani, mentre la dissezione mentale di un oggetto si riferisce solo a questo taglio e non comporta un cambiamento in altre immagini dello stesso oggetto. La sezione mostra cosa si trova nel piano di taglio e cosa si trova dietro di esso.
A seconda del numero di piani secanti la sezione si divide in:
Semplice (con un piano di taglio)
Complesso (con diversi piani di taglio)
A seconda della posizione del piano di taglio rispetto al piano di proiezione orizzontale, le sezioni si dividono in:
ORIZZONTALE – il piano di taglio è parallelo al piano di proiezione orizzontale
VERTICALE - il piano di taglio è perpendicolare al piano di proiezione orizzontale
OBLIQUO - un piano di taglio è un angolo indiretto con un piano orizzontale =) Si chiama sezione VERTICALE frontale se il piano di taglio è parallelo al piano frontale delle proiezioni. E profilo se il piano di taglio è parallelo al piano del profilo delle proiezioni.
I tagli COMPLESSI sono LONGITUDINALI se i piani di taglio sono diretti lungo la lunghezza o l'altezza dell'oggetto. E TRASVERSALE SE i piani di taglio sono diretti PERPENDICOLARI alla lunghezza o all'altezza dell'oggetto.
STEP – se i piani secanti sono paralleli tra loro
ROTTO – se i piani di taglio si intersecano tra loro.
I tagli LOCALI servono a rivelare la struttura interna di un oggetto in un luogo limitato e separato. La SEZIONE LOCALE è evidenziata nella vista da una linea continua, ondulata e sottile.
Designazione dei tagli - La posizione del piano di taglio è indicata da una linea di sezione aperta. I tratti iniziale e finale della linea di sezione non devono intersecare il contorno dell'immagine corrispondente. Sul tratto iniziale e finale devono essere posizionate delle frecce che indicano la direzione della visuale, ad una distanza di 2...3 mm dall'estremità esterna del tratto.
PER UN TAGLIO COMPLESSO, i tratti della linea di sezione aperta vengono disegnati anche in corrispondenza delle pieghe della linea di sezione.
VICINO alle frecce che indicano la direzione della vista, all'esterno dell'angolo sono applicate le lettere maiuscole dell'alfabeto russo. Le designazioni delle lettere sono assegnate in ordine alfabetico senza ripetizioni o omissioni.
L'incisione stessa dovrebbe essere contrassegnata con un'iscrizione come A-A
Se il piano secante coincide con il piano di simmetria dell'oggetto e la sezione viene realizzata al posto della vista corrispondente nella connessione di proiezione, per le sezioni orizzontali, frontali e di profilo non è necessario contrassegnare la posizione del piano secante e il taglio non è accompagnato da un'iscrizione.
Se la linea di contorno di un oggetto coincide con l'asse di simmetria, il confine tra la vista e la sezione è indicato da una linea ondulata, disegnata in modo da preservare l'immagine del bordo.
