Wykład na temat „Test prostopadłości dwóch płaszczyzn”
Idea płaszczyzny w przestrzeni pozwala nam uzyskać np. powierzchnię stołu czy ściany. Jednak stół lub ściana ma skończone wymiary, a płaszczyzna rozciąga się poza jej granice w nieskończoność.Rozważmy dwie przecinające się płaszczyzny. Kiedy się przecinają, tworzą cztery kąty dwuścienne ze wspólną krawędzią.
Przypomnijmy sobie, czym jest kąt dwuścienny.
W rzeczywistości spotykamy obiekty, które mają kształt kąta dwuściennego: na przykład lekko uchylone drzwi lub na wpół otwarta teczka.

Kiedy przecinają się dwie płaszczyzny alfa i beta, otrzymujemy cztery kąty dwuścienne. Niech jeden z kątów dwuściennych będzie równy (phi), wówczas drugi będzie równy (180 0 –), trzeci, czwarty (180 0 -).

α Iβ, 0°< 90 °
Rozważmy przypadek, gdy jeden z kątów dwuściennych wynosi 90 0 .
Następnie wszystkie kąty dwuścienne w tym przypadku są równe 90 0 .
kąt dwuścienny między płaszczyznamiα Iβ,
90°
Wprowadźmy definicję płaszczyzn prostopadłych:
Dwie płaszczyzny nazywamy prostopadłymi, jeśli kąt dwuścienny między nimi wynosi 90°.
Kąt pomiędzy płaszczyznami sigma i epsilon wynosi 90 stopni, co oznacza, że płaszczyzny są prostopadłe
Ponieważ =90°
Podajmy przykłady płaszczyzn prostopadłych.
Ściana i sufit.
Ściana boczna i blat stołu.

Ściana i sufit
Sformułujmy znak prostopadłości dwóch płaszczyzn:
TWIERDZENIE:Jeżeli jedna z dwóch płaszczyzn przechodzi przez linię prostopadłą do drugiej płaszczyzny, to płaszczyzny te są prostopadłe.
Udowodnijmy ten znak.
Pod warunkiem wiadomo, że linia prostaAM leży w płaszczyźnie α, prosta AM jest prostopadła do płaszczyzny β,
Udowodnić: płaszczyzny α i β są prostopadłe.
Dowód:
1) Płaszczyzny α iβ przecinają się wzdłuż prostej AR i AM AR, ponieważ AM β pod warunkiem, to znaczy, że AM jest prostopadła do dowolnej linii prostej leżącej w płaszczyźnie β.
2) Narysujmy linię prostą w płaszczyźnie βAT prostopadleAR.
Otrzymujemy kąt TAM jest kątem liniowym kąta dwuściennego. Ale kąt TAM = 90°, ponieważ MA to β. Zatem αβ.
co było do okazania
TWIERDZENIE:Jeżeli płaszczyzna przechodzi przez linię prostopadłą do innej płaszczyzny, to płaszczyzny te są prostopadłe.

Dany:α, β, AM α, AMβ, AM∩=A
Udowodnij: αβ.
Dowód:
1) α∩β = AR, natomiast AM AR, ponieważ AM β pod warunkiem, to znaczy, że AM jest prostopadła do dowolnej linii prostej leżącej w płaszczyźnie β.
2) ATβ,ATAR.
TAM jest kątem liniowym kąta dwuściennego. TAM = 90°, ponieważ MA β. Zatem αβ.
CO BYŁO DO OKAZANIA
Ze znaku prostopadłości dwóch płaszczyzn mamy ważny wniosek:
UDERZENIE:Płaszczyzna prostopadła do linii, wzdłuż której przecinają się dwie płaszczyzny, jest prostopadła do każdej z tych płaszczyzn.
Udowodnijmy tę zależność: jeśli płaszczyzna gamma jest prostopadła do prostej c, to bazując na równoległości obu płaszczyzn, gamma jest prostopadła do alfa. Podobnie gamma jest prostopadła do beta

Czyli: jeśli α∩β=с i γс, to γα i γβ.
ponieważγс i сα ze znaku prostopadłości γα.
Podobny do γ β
Przeformułujmy ten wniosek dla kąta dwuściennego:
Płaszczyzna przechodząca przez kąt liniowy kąta dwuściennego jest prostopadła do krawędzi i ścian tego kąta dwuściennego. Innymi słowy, jeśli skonstruowaliśmy kąt liniowy kąta dwuściennego, to przechodząca przez niego płaszczyzna jest prostopadła do krawędzi i ścian tego kąta dwuściennego.

Zadanie.
Dane: ΔАВС, С = 90°, АС leży w płaszczyźnie α, kąt pomiędzy płaszczyznami α iABC= 60°, AC = 5 cm, AB = 13 cm.
Znajdź: odległość punktu B od płaszczyzny α.
Rozwiązanie:
1) Skonstruujmy VC α. Wtedy KS jest rzutem słońca na tę płaszczyznę.
2) BC AC (według warunku), co oznacza zgodnie z twierdzeniem o trzech prostopadłych (TPP) KS AC. Dlatego VSK jest kątem liniowym kąta dwuściennego między płaszczyzną α a płaszczyzną trójkąta ABC. Oznacza to, że VSK = 60°.
3) Z ΔBCA zgodnie z twierdzeniem Pitagorasa:
Od ΔVKS: ![]()
Ta lekcja pomoże tym, którzy chcą zrozumieć temat „Znak prostopadłości dwóch płaszczyzn”. Na początku powtórzymy definicję kąta dwuściennego i liniowego. Następnie zastanowimy się, które płaszczyzny nazywamy prostopadłymi i udowodnimy znak prostopadłości dwóch płaszczyzn.
Temat: Prostopadłość prostych i płaszczyzn
Lekcja: Znak prostopadłości dwóch płaszczyzn
Definicja. Kąt dwuścienny to figura utworzona przez dwie półpłaszczyzny, które nie należą do tej samej płaszczyzny i ich wspólną linię prostą a (a jest krawędzią).
Ryż. 1
Rozważmy dwie półpłaszczyzny α i β (ryc. 1). Ich wspólną granicą jest l. Liczba ta nazywana jest kątem dwuściennym. Dwie przecinające się płaszczyzny tworzą cztery kąty dwuścienne o wspólnej krawędzi.
Kąt dwuścienny mierzy się za pomocą kąta liniowego. Wybieramy dowolny punkt na wspólnej krawędzi l kąta dwuściennego. W półpłaszczyznach α i β z tego punktu rysujemy prostopadłe a i b do prostej l i otrzymujemy kąt liniowy kąta dwuściennego.
Proste aib tworzą cztery kąty równe φ, 180° - φ, φ, 180° - φ. Przypomnijmy, że kąt między prostymi jest najmniejszym z tych kątów.
Definicja. Kąt między płaszczyznami jest najmniejszym z kątów dwuściennych utworzonych przez te płaszczyzny. φ jest kątem pomiędzy płaszczyznami α i β, jeśli
Definicja. Dwie przecinające się płaszczyzny nazywane są prostopadłymi (wzajemnie prostopadłymi), jeśli kąt między nimi wynosi 90°.

Ryż. 2
Na krawędzi l wybierany jest dowolny punkt M (rys. 2). Narysujmy dwie prostopadłe linie proste MA = a i MB = b do krawędzi l odpowiednio w płaszczyźnie α i w płaszczyźnie β. Mamy kąt AMB. Kąt AMB jest kątem liniowym kąta dwuściennego. Jeżeli kąt AMB wynosi 90°, to płaszczyzny α i β nazywamy prostopadłymi.
Linia b jest prostopadła do linii l ze względu na konstrukcję. Linia b jest prostopadła do linii a, ponieważ kąt pomiędzy płaszczyznami α i β wynosi 90°. Stwierdzamy, że prosta b jest prostopadła do dwóch przecinających się linii a i l z płaszczyzny α. Oznacza to, że prosta b jest prostopadła do płaszczyzny α.
Podobnie możemy udowodnić, że prosta a jest prostopadła do płaszczyzny β. Linia a jest konstrukcyjnie prostopadła do linii l. Linia a jest prostopadła do linii b, ponieważ kąt pomiędzy płaszczyznami α i β wynosi 90°. Stwierdzamy, że prosta a jest prostopadła do dwóch przecinających się linii b i l z płaszczyzny β. Oznacza to, że prosta a jest prostopadła do płaszczyzny β.
Jeżeli jedna z dwóch płaszczyzn przechodzi przez linię prostopadłą do drugiej płaszczyzny, to płaszczyzny te są prostopadłe.
Udowodnić:

Ryż. 3
Dowód:
Niech płaszczyzny α i β przecinają się na prostej AC (rys. 3). Aby udowodnić, że płaszczyzny są wzajemnie prostopadłe, należy skonstruować między nimi kąt liniowy i pokazać, że kąt ten wynosi 90°.
Prosta AB jest prostopadła do płaszczyzny β, a zatem do prostej AC leżącej w płaszczyźnie β.
Narysujmy prostą AD prostopadłą do prostej AC w płaszczyźnie β. Wtedy BAD jest kątem liniowym kąta dwuściennego.
Prosta AB jest prostopadła do płaszczyzny β, a zatem do prostej AD leżącej w płaszczyźnie β. Oznacza to, że kąt liniowy BAD wynosi 90°. Oznacza to, że płaszczyzny α i β są prostopadłe, co należało udowodnić.
Płaszczyzna prostopadła do prostej, wzdłuż której przecinają się dwie dane płaszczyzny, jest prostopadła do każdej z tych płaszczyzn (rys. 4).
Udowodnić:

Ryż. 4
Dowód:
Prosta l jest prostopadła do płaszczyzny γ, a płaszczyzna α przechodzi przez prostą l. Oznacza to, że zgodnie z prostopadłością płaszczyzn, płaszczyzny α i γ są prostopadłe.
Prosta l jest prostopadła do płaszczyzny γ, a płaszczyzna β przechodzi przez prostą l. Oznacza to, że zgodnie z prostopadłością płaszczyzn, płaszczyzny β i γ są prostopadłe.
Definicja. Kąt dwuścienny to figura utworzona przez linię prostą a i dwie półpłaszczyzny o wspólnej granicy a, które nie należą do tej samej płaszczyzny.
Definicja. Miara stopnia kąta dwuściennego jest miarą stopnia dowolnego z jego kątów liniowych.
Definicja. Dwie przecinające się płaszczyzny nazywamy prostopadłymi, jeżeli kąt między nimi wynosi 90°.
Znak prostopadłości dwóch płaszczyzn.
Nieruchomości.
- W prostopadłościanie wszystkie sześć ścian jest prostokątami.
- Wszystkie kąty dwuścienne prostopadłościanu są kątami prostymi
- Kwadrat przekątnej równoległościanu prostokątnego jest równy sumie kwadratów jego trzech wymiarów.
Zadania i testy na temat „Temat 7. „Kąt dwuścienny. Prostopadłość płaszczyzn.”
- Kąt dwuścienny. Prostopadłość płaszczyzn
- Prostopadłość prostej i płaszczyzny - Prostopadłość prostych i płaszczyzn, ocena 10
Lekcje: 1 Zadania: 10 Testy: 1
- Prostopadłe i ukośne. Kąt między linią prostą a płaszczyzną - Prostopadłość prostych i płaszczyzn, ocena 10
Lekcje: 2 Zadania: 10 Testy: 1
- Równoległość płaszczyzn - Równoległość prostych i płaszczyzn, klasa 10
Lekcje: 1 Zadania: 8 Testy: 1
- Prostopadłe linie - Podstawowe informacje geometryczne 7. klasa
Lekcje: 1 Zadania: 17 Testy: 1
Materiał na ten temat podsumowuje i systematyzuje informacje znane z planimetrii na temat prostopadłości linii prostych. Wskazane jest połączenie badania twierdzeń o związku między równoległością a prostopadłością linii prostych i płaszczyzn w przestrzeni, a także materiału na prostopadłych i nachylonych, z systematycznym powtarzaniem odpowiedniego materiału z planimetrii.
Rozwiązania prawie wszystkich problemów obliczeniowych sprowadzają się do zastosowania twierdzenia Pitagorasa i jego konsekwencji. W wielu zagadnieniach możliwość wykorzystania twierdzenia Pitagorasa lub jego następstw uzasadnia się twierdzeniem o trzech prostopadłych lub własnościami równoległości i prostopadłości płaszczyzn.
Pojęcie płaszczyzn prostopadłych
Kiedy przecinają się dwie płaszczyzny, otrzymujemy kąty dwuścienne o wartości 4 $. Dwa kąty są równe $\varphi $, a dwa pozostałe są równe $(180)^0-\varphi $.
Definicja 1
Kąt między płaszczyznami jest najmniejszym z kątów dwuściennych utworzonych przez te płaszczyzny.
Definicja 2
Dwie przecinające się płaszczyzny nazywamy prostopadłymi, jeśli kąt między tymi płaszczyznami wynosi $90^\circ$ (rys. 1).
Rysunek 1. Płaszczyzny prostopadłe
Znak prostopadłości dwóch płaszczyzn
Twierdzenie 1
Jeżeli prosta płaszczyzny jest prostopadła do innej płaszczyzny, to płaszczyzny te są do siebie prostopadłe.
Dowód.
Dajmy sobie płaszczyzny $\alpha $ i $\beta $, które przecinają się na prostej $AC$. Niech prosta $AB$ leżąca w płaszczyźnie $\alpha $ będzie prostopadła do płaszczyzny $\beta $ (rys. 2).

Rysunek 2.
Ponieważ prosta $AB$ jest prostopadła do płaszczyzny $\beta$, jest także prostopadła do prostej $AC$. Narysujmy dodatkowo prostą $AD$ w płaszczyźnie $\beta$, prostopadłej do prostej $AC$.
Stwierdzamy, że kąt $BAD$ jest kątem liniowym kąta dwuściennego, równym $90^\circ$. Oznacza to, że z definicji 1 kąt pomiędzy płaszczyznami wynosi $90^\circ$, co oznacza, że płaszczyzny te są prostopadłe.
Twierdzenie zostało udowodnione.
Z twierdzenia tego wynika następujące twierdzenie.
Twierdzenie 2
Jeżeli płaszczyzna jest prostopadła do prostej, wzdłuż której przecinają się dwie inne płaszczyzny, to jest również prostopadła do tych płaszczyzn.
Dowód.
Dano nam dwie płaszczyzny $\alpha $ i $\beta $ przecinające się wzdłuż prostej $c$. Płaszczyzna $\gamma $ jest prostopadła do prostej $c$ (rys. 3)

Rysunek 3.
Ponieważ prosta $c$ należy do płaszczyzny $\alpha $ i płaszczyzna $\gamma $ jest prostopadła do prostej $c$, to zgodnie z Twierdzeniem 1 płaszczyzny $\alpha $ i $\gamma $ są prostopadłe.
Ponieważ prosta $c$ należy do płaszczyzny $\beta $, a płaszczyzna $\gamma $ jest prostopadła do prostej $c$, to zgodnie z Twierdzeniem 1 płaszczyzny $\beta $ i $\gamma $ są prostopadłe.
Twierdzenie zostało udowodnione.
W przypadku każdego z tych twierdzeń prawdziwe są także stwierdzenia odwrotne.
Przykładowe problemy
Przykład 1
Dajmy sobie równoległościan prostokątny $ABCDA_1B_1C_1D_1$. Znajdź wszystkie pary płaszczyzn prostopadłych (ryc. 5).

Rysunek 4.
Rozwiązanie.
Z definicji prostokątnej płaszczyzny równoległościennej i prostopadłej wynika, że widzimy osiem par płaszczyzn prostopadłych do siebie: $(ABB_1)$ i $(ADD_1)$, $(ABB_1)$ i $(A_1B_1C_1)$, $( ABB_1)$ i $(BCC_1) $, $(ABB_1)$ i $(ABC)$, $(DCC_1)$ i $(ADD_1)$, $(DCC_1)$ i $(A_1B_1C_1)$, $(DCC_1) $ i $(BCC_1)$, $(DCC_1)$ i $(ABC)$.
Przykład 2
Dano nam dwie wzajemnie prostopadłe płaszczyzny. Z punktu na jednej płaszczyźnie poprowadzono prostopadłą do drugiej płaszczyzny. Udowodnić, że prosta ta leży na danej płaszczyźnie.
Dowód.
Dano nam płaszczyzny prostopadłe $\alpha $ i $\beta $ przecinające się wzdłuż prostej $c$. Z punktu $A$ płaszczyzny $\beta $ poprowadzono prostopadłą $AC$ do płaszczyzny $\alpha $. Załóżmy, że $AC$ nie leży w płaszczyźnie $\beta$ (rys. 6).
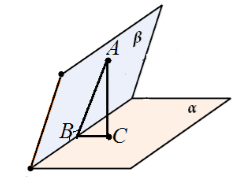
Rysunek 5.
Rozważmy trójkąt $ABC$. Jest prostokątny o kącie prostym $ACB$. Dlatego $\kąt ABC\ne (90)^0$.
Z drugiej jednak strony $\kąt ABC$ jest kątem liniowym kąta dwuściennego utworzonego przez te płaszczyzny. Oznacza to, że kąt dwuścienny utworzony przez te płaszczyzny nie jest równy 90 stopni. Stwierdzamy, że kąt pomiędzy płaszczyznami nie jest równy $90^\circ$. Sprzeczność. Zatem $AC$ leży w płaszczyźnie $\beta$.
Konstrukcja dwóch wzajemnie prostopadłych płaszczyzn. Jak wiadomo, płaszczyzny są prostopadłe, jeżeli prosta należąca do jednej płaszczyzny jest prostopadła do innej płaszczyzny. Zatem płaszczyznę prostopadłą do danej można poprowadzić przez linię prostopadłą do danej płaszczyzny lub prostopadłą do prostej leżącej w danej płaszczyźnie.
Pokazane na ryc. 4.12 Płaszczyzny (płaszczyzna trójkąta ABC i płaszczyzna P) są wzajemnie prostopadłe, ponieważ płaszczyzna P jest prostopadła do prostej A1 leżącej w płaszczyźnie trójkąta. Rzut płaszczyzny P przechodzącej przez linię z rzutami m 2 n 2, m 1 n 1 i prostopadłej do płaszczyzny określonej przez rzuty a 2 b 2 c 2, a 1 b 1 c 1 trójkąta pokazano na rysunku Figa. 4.12.
Konstrukcja: 1. Narysuj główne linie płaszczyzny, C1 - pozioma, C2 - czołowa.
2. Przez dowolny punkt E (położony na zewnątrz trójkąta ABC) poprowadź linię prostą EF prostopadłą do głównych linii płaszczyzny (c 2 f 2 jest prostopadłe do c 2 2 2 i c 1 f 1 jest prostopadłe do 1 1 1).
3. Przez punkt N poprowadź dowolną prostą EM przecinającą się z EF, otrzymamy płaszczyznę P wyznaczoną przez dwie przecinające się proste (EM X EF).
Zatem płaszczyzna P(ME X EF) jest prostopadła do płaszczyzny Q(trójkąt ABC).
Należy zauważyć, że w przypadku płaszczyzn wzajemnie prostopadłych w położeniu ogólnym ich ślady o tej samej nazwie nigdy nie są prostopadłe. Jeżeli jednak jedna z podanych płaszczyzn (lub obie) jest płaszczyzną ogólną, to wzajemna prostopadłość na wykresie jednej pary ich śladów wskazuje na prostopadłość płaszczyzn w przestrzeni.
18) Linię prostą przecięcia dwóch płaszczyzn można wyznaczyć poprzez ich dwa wspólne punkty. W tym celu należy wyznaczyć punkty przecięcia dowolnych dwóch prostych jednej płaszczyzny z inną płaszczyzną lub punkty przecięcia prostej na każdej z płaszczyzn z inną płaszczyzną
Kolejność budowy:
Linię przecięcia dwóch płaszczyzn można znaleźć, korzystając przy rozwiązywaniu z pomocniczych płaszczyzn tnących. Zwykle wybiera się płaszczyzny projekcyjne (często poziome lub czołowe)
Wybierz dowolną sieczną pomocniczą poziomą płaszczyznę Ф1, która przecina dane płaszczyzny wzdłuż linii prostych (12 i 34), które (na p1 przecinają się w punkcie k)
Druga sieczna płaszczyzna pozioma przecina dane płaszczyzny także wzdłuż poziomych, one z kolei przecinają się w punkcie E
Prosta KE jest linią przecięcia danych płaszczyzn.
Rozważmy rozwiązanie tego problemu na płaskim rysunku.
I etap rozwiązania Do skonstruowania punktu M wykorzystuje się poziomo wystającą płaszczyznę - mediator ("), który obejmuje bok AB trójkąta ABC.
II etap rozwiązania Konstruujemy linię przecięcia (na rysunku wyznaczają ją punkty 1 i 2) płaszczyzny pośredniej (”) i płaszczyzny DEK.
III etap rozwiązania Znajdź punkt M przecięcia linii 1 - 2 z linią AB.
Znaleziono jeden punkt M żądanej linii przecięcia.
Do skonstruowania punktu N wykorzystuje się wystającą poziomo płaszczyznę (”), która obejmuje bok AC trójkąta ABC.
Konstrukcje są podobne do poprzednich.
Wyznaczanie widoczności na płaszczyźnie H odbywa się za pomocą poziomo konkurujących ze sobą punktów 4 i 8
Punkt 4 znajduje się nad punktem 8 (4" i 8"), zatem na płaszczyźnie H część trójkąta DEK, położona w kierunku punktu 4, obejmuje część trójkąta ABC, położoną od linii przecięcia w kierunku punktu 8. Za pomocą wyznaczana jest para frontalnie rywalizujących punktów 6 i 7 z widzialnością na płaszczyźnie V.

Przecięcie dwóch wystających czołowo płaszczyzn (?)
Przecięcie dwóch poziomo wystających płaszczyzn (?)
19) Cięcie to obraz przedmiotu rozcięty mentalnie w jednej lub kilku płaszczyznach, przy czym rozcięcie mentalne przedmiotu dotyczy tylko tego cięcia i nie pociąga za sobą zmiany w innych obrazach tego samego przedmiotu. Sekcja pokazuje co znajduje się w płaszczyźnie cięcia i co znajduje się za nią.
W zależności od liczby siecznych płaszczyzn przekrój dzieli się na:
Prosty (z jedną płaszczyzną cięcia)
Złożone (z kilkoma płaszczyznami cięcia)
W zależności od położenia płaszczyzny cięcia względem płaszczyzny rzutu poziomego przekroje dzielą się na:
POZIOMA – płaszczyzna cięcia jest równoległa do poziomej płaszczyzny rzutowania
PIONOWA - płaszczyzna cięcia jest prostopadła do poziomej płaszczyzny rzutowania
SKOŚNA - płaszczyzna cięcia to jakiś kąt pośredni z płaszczyzną poziomą =) Nazywa się przekrój PIONOWY czołowy jeżeli płaszczyzna cięcia jest równoległa do przedniej płaszczyzny występów. I profil jeśli płaszczyzna cięcia jest równoległa do płaszczyzny profilu występów.
Cięcia KOMPLEKSOWE mają charakter WZDŁUŻNY, jeśli płaszczyzny cięcia są skierowane wzdłuż długości lub wysokości przedmiotu. ORAZ POPRZECZNE JEŚLI płaszczyzny cięcia są skierowane PROSTOPADLE do długości lub wysokości obiektu.
KROK – jeśli sieczne płaszczyzny są do siebie równoległe
ZŁAMANY – jeśli płaszczyzny cięcia przecinają się.
Cięcia LOKALNE służą ukazaniu wewnętrznej struktury obiektu w wydzielonym, ograniczonym miejscu. SEKCJA LOKALNA jest wyróżniona w widoku ciągłą, falistą, cienką linią.
Oznaczenie cięć - Położenie płaszczyzny cięcia jest oznaczone otwartą linią przekroju. Początkowe i końcowe pociągnięcia linii przekroju nie powinny przecinać konturu odpowiedniego obrazu. Na kreskach początkowej i końcowej należy umieścić strzałki wskazujące kierunek patrzenia, w odległości 2...3 mm od zewnętrznego końca kreski.
W PRZYPADKU ZŁOŻONEGO CIĘCIA pociągnięcia linii otwartego przekroju są również rysowane na zagięciach linii przekroju.
W POBLIŻU strzałek wskazujących kierunek patrzenia, na zewnętrznej stronie narożnika znajdują się wielkie litery alfabetu rosyjskiego. Oznaczenia literowe nadawane są w kolejności alfabetycznej, bez powtórzeń i pominięć.
Samo nacięcie powinno być oznaczone napisem np. A-A
Jeżeli sieczna płaszczyzna pokrywa się z płaszczyzną symetrii obiektu, a przekrój jest wykonywany w miejscu odpowiedniego widoku w połączeniu rzutowym, to w przypadku przekrojów poziomych, czołowych i profilowych nie ma potrzeby zaznaczania położenia siecznej płaszczyzny a rozcięciu nie towarzyszy napis.
Jeżeli kontur obiektu pokrywa się z osią symetrii, wówczas granicę między widokiem a przekrojem wyznacza linia falista, narysowana w taki sposób, aby zachować obraz krawędzi.
