Iš grafikų matyti, kad:
- Sinuso ir kosinuso grafikai svyruoja nuo -1 iki 1
- Kosinuso kreivė turi tokią pačią formą kaip sinuso kreivė, bet jos atžvilgiu yra pasislinkusi 90 o
- Sinuso ir kosinuso kreivės yra ištisinės ir kartojasi 360 o periodu, liestinės kreivė turi nutrūkimų ir kartojasi su 180 o periodu.
Ant pav. kairėje pavaizduotos statmenos ašys XX" ir YY"; susikertanti ištakoje O. Dirbant su grafikais matavimai į dešinę ir aukštyn nuo O laikomi teigiamais, į kairę ir žemyn nuo O – neigiamais. Leiskite OA laisvai suktis O atžvilgiu. Kai OA pasukama prieš laikrodžio rodyklę, išmatuotas kampas laikomas teigiamu, o sukamas pagal laikrodžio rodyklę – neigiamas.
Tvarkaraštis. teigiamas ar neigiamas
kryptimi sukamaisiais judesiais.
Tegul OA sukasi prieš laikrodžio rodyklę taip, kad Θ 1 būtų bet koks kampas pirmajame kvadrante, ir pastatykite statmeną AB, kad gautumėte statųjį trikampį OAB pav. paliko. Kadangi visos trys trikampio kraštinės yra teigiamos, trigonometrinės funkcijos sinusas, kosinusas ir liestinė pirmajame kvadrante bus teigiamos. (Atkreipkite dėmesį, kad OA ilgis visada yra teigiamas, nes tai yra apskritimo spindulys.)
Tegul OA sukasi toliau taip, kad Θ 2 būtų bet koks kampas antrajame kvadrante, ir sukonstruokite AC taip, kad susidarytų stačiakampis trikampis OAC. Tada sin Θ 2 =+/+ = +; cos Θ 2 =+/- = -; tg Θ 2 =+/- = -. Tegul OA sukasi toliau taip, kad Θ 3 būtų bet koks trečiojo kvadranto kampas, ir sukonstruokite AD taip, kad susidarytų stačiakampis trikampis OAD. Tada sin Θ 3 = -/+ = -; cos Θ 3 = -/+ = -; tg Θ 3 = -/- =+ .
Tvarkaraštis. Kampų pastatymas
įvairūs kvadrantai.
Tegul OA sukasi toliau taip, kad Θ 4 būtų bet koks ketvirtojo kvadranto kampas, ir sukonstruokite AE taip, kad susidarytų stačiakampis trikampis OAE. Tada sin Θ 4 = -/+= -; cos Θ 4 =+/+=+; tg Θ 4 = -/+= -.
Pirmajame kvadrante visos trigonometrinės funkcijos turi teigiamas reikšmes, antrajame – teigiamas tik sinusas, trečiajame – tik liestinė, ketvirtajame – tik kosinusas, kuris parodytas fig. paliko.
Žinios apie savavališko dydžio kampus būtinos, kai, pavyzdžiui, randame visus kampus nuo 0 o iki 360 o, kurių sinusas yra, tarkime, 0,3261. Jei į skaičiuotuvą įvedate 0,3261 ir paspaudžiate sin -1 mygtuką, gauname atsakymą 19,03 o. Tačiau yra antras kampas nuo 0 o iki 360 o, kurio skaičiuotuvas nerodys. Sinusas taip pat yra teigiamas antrajame kvadrante. Kitas kampas parodytas fig. žemiau kaip kampas Θ, kur Θ=180 o - 19,03 o = 160,97 o . Taigi 19,03 o ir 160,97 o yra kampai diapazone nuo 0 o iki 360 o, kurių sinusas yra 0,3261.
Būk atsargus! Skaičiuoklė pateikia tik vieną iš šių reikšmių. Antroji vertė turėtų būti nustatyta pagal savavališko dydžio kampų teoriją.
1 pavyzdys
Raskite visus kampus nuo 0 o iki 360 o, kurių sinusas yra -0,7071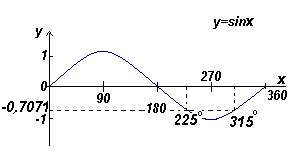 
Sprendimas:
Kampai, kurių sinusas yra -0,7071 o, yra trečiajame ir ketvirtajame kvadrantuose, nes tuose kvadrantuose sinusas yra neigiamas (žr. paveikslą kairėje).
Tvarkaraštis. Visų kampų paieška pagal
duota sinuso reikšmė (pavyzdys)
Iš toliau pateikto paveikslo Θ = arcsin 0,7071 = 45 o . Du kampai diapazone nuo 0 o iki 360 o, kurių sinusas yra -0,7071, yra 180 o +45 o \u003d 225 o ir 360 o - 45 o \u003d 315 o.
.gif)
Pastaba. Skaičiuoklė pateikia tik vieną atsakymą.
Tvarkaraštis. Visų kampų paieška pagal
duota sinuso reikšmė (pavyzdys)
2 pavyzdys
Raskite visus kampus nuo 0 o iki 360 o, kurių liestinė yra 1,327. 
Sprendimas:
Pirmajame ir trečiajame kvadrantuose liestinė yra teigiama – pav. paliko.
Tvarkaraštis. Visų kampų paieška pagal
Iš žemiau esančio paveikslo Θ = arctan1,327= 53 o . .gif)
Du kampai diapazone nuo 0 o iki 360 o, kurių liestinė yra 1,327, yra 53 o ir 180 o + 53 o, t.y. 233o.
Tvarkaraštis. Visų kampų paieška pagal
duota liestinės reikšmė (pavyzdys)
Leiskite OR pav. kairėje yra vienetinio ilgio vektorius, laisvai besisukantis prieš laikrodžio rodyklę aplink O. Vienu apsisukimu susidaro apskritimas, parodytas fig. ir padalintas iš 15 o sektorių. Kiekvienas spindulys turi horizontalią ir vertikalią sudedamąsias dalis. Pavyzdžiui, 30 o vertikalus komponentas yra TS, o horizontalus komponentas yra OS. Iš trigonometrinių funkcijų apibrėžimo
sin30 o =TS/TO=TS/1, t.y. TS=sin30o Ir cos30 o =OS/TO=OS/1, t.y. OS = cos30o
Vertikalioji komponentė TS gali būti nubraižyta kaip T"S", kuri yra lygi vertei, atitinkančiai 30° kampą y ir x kampo diagramoje. Jei visi vertikalūs komponentai, tokie kaip TS, perkeliami į grafiką, bus gauta sinusoidė, parodyta Fig. aukštesnė.
Jei visi horizontalūs komponentai, pvz., OS, yra projektuojami į y ir x diagramą, gausite kosinuso bangą. Šias projekcijas lengva vizualizuoti perbraižant apskritimą, kurio spindulys ARBA ir kampai iš vertikalios pusės, kaip parodyta paveikslėlyje kairėje.
Iš pav. kairėje pusėje matote, kad sinusoidė turi tokią pačią formą kaip ir kosinuso banga, bet pasislinkusi 90 o .
 |
 |
 |
 |
Periodinės funkcijos ir laikotarpis
Kiekviena iš funkcijų grafikų, parodytų keturiuose Fig. aukščiau, kartojasi didėjant kampui A, todėl jie vadinami periodines funkcijas.
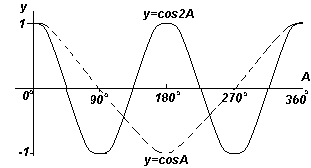
Funkcijos y=sinA ir y=cosA kartojasi kas 360 o (arba 2π radianus), todėl 360 o vadinama laikotarpįšias funkcijas. Funkcijos y=sin2A ir y=cos2A kartojasi kas 180 o (arba π radianų), taigi 180 o yra šių funkcijų periodas.
Apskritai, jei y=sinpA ir y=cospA (kur p yra konstanta), tai funkcijos periodas yra 360 o /p (arba 2π/p radianų). Todėl, jei y=sin3A, tai šios funkcijos periodas yra 360 o /3= 120 o , jei y=cos4A, tai šios funkcijos periodas yra 360 o /4= 90 o .
Amplitudė
Amplitudė vadinama maksimalia sinusoido verte. Kiekvienos iš 1–4 grafikų amplitudė yra +1 (t. y. jos svyruoja nuo +1 iki -1). Tačiau, jei y=4sinA, kiekviena sinA reikšmė padauginama iš 4, taigi maksimali amplitudės reikšmė yra 4. Panašiai, kai y=5cos2A, amplitudė yra 5, o periodas yra 360 o /2= 180 o .
3 pavyzdys
Sukurkite y=3sin2A diapazone nuo A= 0 o iki A=360 o . 
Sprendimas:
Amplitudė =3, periodas = 360 o /2 =180 o .
4 pavyzdys
Nubraižykite y=4cos2x diapazone nuo x=0 o iki x=360 o 
Sprendimas:
Amplitudė = 4. periodas = 360 o /2 =180 o .
Atsilikimo ir švino kampai
Sinuso ir kosinuso kreivės ne visada prasideda nuo 0 o . Kad būtų atsižvelgta į šią aplinkybę, periodinė funkcija vaizduojama kaip y=sin(A± α), kur α yra fazės poslinkis y=sinA ir y=cosA atžvilgiu.
.gif)
Sudarę reikšmių lentelę, galite nubraižyti funkciją y=sin(A-60 o), parodytą fig. paliko. Jei y=sinA kreivė prasideda nuo 0 o , tai kreivė y=sin(A-60 o ) prasideda nuo 60 o (ty jos nulinė reikšmė yra 60 o į dešinę). Taigi sakoma, kad y = sin(A-60 o) vėlai y=sinA atžvilgiu 60°.
Tvarkaraštis. y=sin(A-60 o) (sinuso banga).
.gif)
Sudarę reikšmių lentelę, galite nubraižyti funkciją y=cos(A+45 o), parodytą fig. žemiau.
Jei kreivė y=cosA prasideda nuo 0 o , tai kreivė y=cos(A+45 o) prasideda 45 o į kairę (ty jos nulinė reikšmė yra 45 o anksčiau).
Taigi sakoma, kad diagrama yra y=cos(A+45 o) prieš diagrama y=cosA 45° kampu.
Tvarkaraštis. y=cos(A+45 o) (kosinusas).
Apskritai grafikas y=sin(A-α) atsilieka nuo y=sinA kampu α.
Kosinuso banga yra tokios pat formos kaip sinusoidė, bet prasideda 90 o į kairę, t.y. lenkia ją 90 o . Todėl cosA=sin(A+90o).
5 pavyzdys
Nubraižykite y=5sin(A+30o) intervale nuo A=0o iki A=360o
.gif)
Sprendimas:
Amplitudė = 5, periodas = 360 o /1 = 360 o .
5sin(A+30 o) pirmauja 5sinA 30 o t.y. prasideda 30 o anksčiau.
Grafikas y=5sin(A+30 o) (sinusoidas).
6 pavyzdys
Nubraižykite y=7sin(2A-π/3) intervale nuo A=0 o iki A=360 o . 
Sprendimas:
Amplitudė = 7, periodas = 2π/2= π radianai
Apskritai y=sin(pt-α) atsilieka nuo y=sinpt α/p, todėl 7sin(2A-π/3) atsilieka nuo 7sin2A (π/3)/2, t.y. už π/6 radianų arba 30 o
Asin(ωt±α) formos sinusoidas. fazės kampas. Fazės poslinkis. 
Leiskite ARBA pav. kairėje yra vektorius, laisvai besisukantis prieš laikrodžio rodyklę aplink O ω radianų/s greičiu. Besisukantis vektorius vadinamas fazės vektorius. Po t sekundžių OR pasisuks kampu ωt radianais (paveiksle kairėje tai kampas TOR). Jeigu ST statomas statmenai OR, tai sinωt=ST/OT, t.y. ST = OTsinωt.
Jei visi tokie vertikalūs komponentai yra projektuojami į y ir ωt diagramą, bus gauta sinusoidė su amplitudė OR.
Jei fazės vektorius ARBA padaro vieną apsisukimą (t. y. 2π radianus) per T sekundes, tai kampinis greitis ω=2π/T rad/s, iš kur
Т=2π/ ω (s), kur
T yra laikotarpį
Vadinamas pilnų laikotarpių, praeinančių per 1 sekundę, skaičius dažnis f.
Dažnis = (periodų skaičius)/(sekundė) = 1/ T = ω/2π Hz, tie. f= ω/2π Hz
Todėl kampinis greitis
ω=2πf rad/s.
Jei apskritai sinusoidinė funkcija atrodo taip y=sin(ωt± α), tada
A – amplitudė
ω – kampinis greitis
2π/ ω - periodas T, s
ω/2π - dažnis f, Hz
α yra švino arba vėlavimo kampas (santykis su y=Аsinωt) radianais, jis taip pat vadinamas faziniu kampu.
7 pavyzdys
Kintamoji srovė pateikiama kaip i=20sin(90πt+0,26) amperų. Nustatykite amplitudę, periodą, dažnį ir fazės kampą (laipsniais)
Sprendimas:
i \u003d 20sin (90πt + 0,26) A, todėl
amplitudė yra 20 A
kampinis greitis ω= 90π, todėl
laikotarpis T= 2π/ ω = 2π/ 90π = 0,022 s = 22 ms
dažnis f\u003d 1 / T \u003d 1 / 0,022 \u003d 45,46 Hz
fazės kampas α= 0,26 rad. \u003d (0,26 * 180 / π) o \u003d 14,9 o.
8 pavyzdys
Virpesių mechanizmo didžiausias poslinkis yra 3 m, o dažnis - 55 Hz. Laike t=0 poslinkis yra 100 cm. Poslinkį išreikškite bendra forma Аsin(ωt± α).
Sprendimas
Amplitudė = didžiausias poslinkis = 3 m
Kampinis greitis ω=2πf = 2π(55) = 110 rad/s
Todėl poslinkis yra 3sin(110πt + α) m.
Esant t = 0 poslinkis = 100 cm = 1 m.
Todėl 1= 3sin(0 + α), t.y. sinα=1/3=0,33
Todėl α=arcsin0,33=19 o
Taigi poslinkis yra 3sin(110 πt + 0,33).
9 pavyzdys
Momentinės įtampos reikšmė kintamosios srovės grandinėje bet kuriomis t sekundėmis pateikiama kaip v=350sin(40πt-0,542)V. Rasti:
a) Amplitudė, periodas, dažnis ir fazės kampas (laipsniais)
b) įtampos reikšmė, kai t = 0
c) įtampos vertė esant t = 10 ms
d) laikas, per kurį įtampa pirmą kartą pasiekia 200 V. 
Sprendimas:
a) Amplitudė 350 V, kampinis greitis ω=40π
Vadinasi,
laikotarpis Т=2π/ ω=2π/40π=0,05 s =50 ms
dažnis f=1/T=1/0,05=20 Hz
fazės kampas \u003d 0,542 rad (0,542 * 180 / π) \u003d 31 o su vėlavimu, palyginti su v \u003d 350sin (40πt)
b) Jei t \u003d 0, tada v \u003d 350sin (0-0,542) \u003d 350sin (-31 o) \u003d -180,25 V
c) Jei t \u003d 10 ms, tada v \u003d 350sin (40π10 / 10 3 -0,542) \u003d 350sin (0,714) \u003d 350sin41 o \u003d V 22
d) Jei v = 200 IR, tada 200 = 350 sin(40πt-0,542) 200/350 = sin(40πt-0,542)
Tvarkaraštis. Virpesių mechanizmas
(pavyzdys, sinusoidas).
v=350sin(40πt-0,542) Todėl (40πt-0,542)=arcsin200/350=35 o arba 0,611 rad.
40πt= 0,611+0,542=1,153.
Taigi, jei v = 200 V, laikas t = 1,153/40π = 9,179 ms
Trigonometrinės kreivės. Sinusoidas. Kosinuso banga. Tangentoidinis. Kotangentoidinis.
Pagal numatytuosius nustatymus visi A kampai yra laipsniais. Visos sinusų, kosinusų, liestinių, kotangentų verčių lentelės ir formulės (). Visose ribų ir serijos plėtimų formulėse kampai yra radianais.
Funkcijų y=sinA, y=cosA, y=tgA, sukurtų diapazonui nuo 0 o iki 360 o , grafikai pateikti toliau pateiktuose paveikslėliuose.
Iš grafikų matyti, kad:
- Sinuso ir kosinuso grafikai svyruoja nuo -1 iki 1
- Kosinuso kreivė turi tokią pačią formą kaip sinuso kreivė, bet jos atžvilgiu yra pasislinkusi 90 o
- Sinuso ir kosinuso kreivės yra ištisinės ir kartojasi 360 o periodu, liestinės kreivė turi nutrūkimų ir kartojasi su 180 o periodu.
Ant pav. kairėje pavaizduotos statmenos ašys XX’ ir YY’; susikertanti ištakoje O. Dirbant su grafikais matavimai į dešinę ir aukštyn nuo O laikomi teigiamais, į kairę ir žemyn nuo O – neigiamais. Leiskite OA laisvai suktis O atžvilgiu. Kai OA pasukama prieš laikrodžio rodyklę, išmatuotas kampas laikomas teigiamu, o sukamas pagal laikrodžio rodyklę – neigiamas.
Tvarkaraštis. teigiamas ar neigiamas
kryptimi sukamaisiais judesiais.
Tegul OA sukasi prieš laikrodžio rodyklę taip, kad Θ 1 būtų bet koks kampas pirmajame kvadrante, ir sukonstruokite statmeną AB, kad gautumėte stačiakampį trikampį OAB Fig. paliko. Kadangi visos trys trikampio kraštinės yra teigiamos, trigonometrinės funkcijos sinusas, kosinusas ir liestinė pirmajame kvadrante bus teigiamos. (Atkreipkite dėmesį, kad OA ilgis visada yra teigiamas, nes tai yra apskritimo spindulys.)
Tegul OA sukasi toliau taip, kad Θ 2 būtų bet koks kampas antrajame kvadrante, ir sukonstruokite AC taip, kad susidarytų stačiakampis trikampis OAC. Tada sin Θ 2 =+/+ = +; cos Θ 2 =+/- = -; tg Θ 2 =+/- = -. Tegul OA sukasi toliau taip, kad Θ 3 būtų bet koks trečiojo kvadranto kampas, ir sukonstruokite AD taip, kad susidarytų stačiakampis trikampis OAD. Tada sin Θ 3 = -/+ = -; cos Θ 3 = -/+ = -; tg Θ 3 = -/- =+ .
Tvarkaraštis. Kampų pastatymas
įvairūs kvadrantai.
Pirmajame kvadrante visos trigonometrinės funkcijos turi teigiamas reikšmes, antrajame – teigiamas tik sinusas, trečiajame – tik liestinė, ketvirtajame – tik kosinusas, kuris parodytas fig. paliko.
Žinios apie savavališko dydžio kampus būtinos, kai, pavyzdžiui, randame visus kampus nuo 0 o iki 360 o, kurių sinusas yra, tarkime, 0,3261. Jei į skaičiuotuvą įvedate 0,3261 ir paspaudžiate sin -1 mygtuką, gauname atsakymą 19,03 o. Tačiau yra antras kampas nuo 0 o iki 360 o, kurio skaičiuotuvas nerodys. Sinusas taip pat yra teigiamas antrajame kvadrante. Kitas kampas parodytas fig. žemiau kaip kampas Θ, kur Θ=180 o - 19,03 o = 160,97 o . Taigi 19,03 o ir 160,97 o yra kampai diapazone nuo 0 o iki 360 o, kurių sinusas yra 0,3261.
Būk atsargus! Skaičiuoklė pateikia tik vieną iš šių reikšmių. Antroji vertė turėtų būti nustatyta pagal savavališko dydžio kampų teoriją.
1 pavyzdys
Raskite visus kampus nuo 0 o iki 360 o, kurių sinusas yra -0,7071
Sprendimas:
Kampai, kurių sinusas yra -0,7071 o, yra trečiajame ir ketvirtajame kvadrantuose, nes tuose kvadrantuose sinusas yra neigiamas (žr. paveikslą kairėje).
Tvarkaraštis. Visų kampų paieška pagal
duota sinuso reikšmė (pavyzdys)
Iš toliau pateikto paveikslo Θ = arcsin 0,7071 = 45 o . Du kampai diapazone nuo 0 o iki 360 o, kurių sinusas yra -0,7071, yra 180 o +45 o \u003d 225 o ir 360 o - 45 o \u003d 315 o.
Pastaba. Skaičiuoklė pateikia tik vieną atsakymą.
Tvarkaraštis. Visų kampų paieška pagal
duota sinuso reikšmė (pavyzdys)
2 pavyzdys
Raskite visus kampus nuo 0 o iki 360 o, kurių liestinė yra 1,327.
Sprendimas:
Pirmajame ir trečiajame kvadrantuose liestinė yra teigiama – pav. paliko.
Tvarkaraštis. Visų kampų paieška pagal
Iš žemiau esančio paveikslo Θ = arctan1,327= 53 o .
Du kampai diapazone nuo 0 o iki 360 o, kurių liestinė yra 1,327, yra 53 o ir 180 o + 53 o, t.y. 233o.
Tvarkaraštis. Visų kampų paieška pagal
duota liestinės reikšmė (pavyzdys)
Leiskite ARBA pav. kairėje yra vienetinio ilgio vektorius, laisvai besisukantis prieš laikrodžio rodyklę aplink O. Vienu apsisukimu susidaro apskritimas, parodytas fig. ir padalintas iš 15 o sektorių. Kiekvienas spindulys turi horizontalią ir vertikalią sudedamąsias dalis. Pavyzdžiui, 30 o vertikalus komponentas yra TS, o horizontalus komponentas yra OS.
Iš trigonometrinių funkcijų apibrėžimo
sin30 o =TS/TO=TS/1, t.y. TS=sin30o Ir cos30 o =OS/TO=OS/1, t.y. OS = cos30o
Vertikalioji komponentė TS gali būti nubraižyta kaip T'S', kuri yra lygi vertei, atitinkančiai 30° kampą y ir x kampo diagramoje. Jei visi vertikalūs komponentai, tokie kaip TS, perkeliami į grafiką, bus gauta sinusoidė, parodyta Fig. aukštesnė.
Jei visi horizontalūs komponentai, pvz., OS, yra projektuojami į y ir x diagramą, gausite kosinuso bangą. Šias projekcijas lengva vizualizuoti perbraižant apskritimą, kurio spindulys ARBA ir kampai iš vertikalios pusės, kaip parodyta paveikslėlyje kairėje.
Iš pav. kairėje pusėje matote, kad sinusoidė turi tokią pačią formą kaip ir kosinuso banga, bet pasislinkusi 90 o .
Kiekviena iš funkcijų grafikų, parodytų keturiuose Fig. aukščiau, kartojasi didėjant kampui A, todėl jie vadinami periodines funkcijas.
Funkcijos y=sinA ir y=cosA kartojasi kas 360 o (arba 2π radianus), todėl 360 o vadinama laikotarpįšias funkcijas. Funkcijos y=sin2A ir y=cos2A kartojasi kas 180 o (arba π radianų), taigi 180 o yra šių funkcijų periodas.
Apskritai, jei y=sinpA ir y=cospA (kur p yra konstanta), tai funkcijos periodas yra 360 o /p (arba 2π/p radianų). Todėl, jei y=sin3A, tai šios funkcijos periodas yra 360 o /3= 120 o , jei y=cos4A, tai šios funkcijos periodas yra 360 o /4= 90 o .
Amplitudė
Amplitudė vadinama maksimalia sinusoido verte. Kiekvienos iš 1–4 grafikų amplitudė yra +1 (t. y. jos svyruoja nuo +1 iki -1). Tačiau, jei y=4sinA, kiekviena sinA reikšmė padauginama iš 4, taigi maksimali amplitudės reikšmė yra 4. Panašiai, kai y=5cos2A, amplitudė yra 5, o periodas yra 360 o /2= 180 o .
3 pavyzdys
Sukurkite y=3sin2A diapazone nuo A= 0 o iki A=360 o .
Sprendimas:
Amplitudė =3, periodas = 360 o /2 =180 o .
4 pavyzdys
Nubraižykite y=4cos2x diapazone nuo x=0 o iki x=360 o
Sprendimas:
Amplitudė = 4. periodas = 360 o /2 =180 o .
Sinuso ir kosinuso kreivės ne visada prasideda nuo 0 o . Kad būtų atsižvelgta į šią aplinkybę, periodinė funkcija vaizduojama kaip y=sin(A± α), kur α yra fazės poslinkis y=sinA ir y=cosA atžvilgiu.
Sudarę reikšmių lentelę, galite nubraižyti funkciją y=sin(A-60 o), parodytą fig. paliko. Jei y=sinA kreivė prasideda nuo 0 o , tai kreivė y=sin(A-60 o ) prasideda nuo 60 o (ty jos nulinė reikšmė yra 60 o į dešinę). Taigi sakoma, kad y = sin(A-60 o) vėlai y=sinA atžvilgiu 60°.
Tvarkaraštis. y=sin(A-60 o) (sinuso banga).
Sudarę reikšmių lentelę, galite nubraižyti funkciją y=cos(A+45 o), parodytą fig. žemiau.
Jei kreivė y=cosA prasideda nuo 0 o , tai kreivė y=cos(A+45 o) prasideda 45 o į kairę (ty jos nulinė reikšmė yra 45 o anksčiau).
Taigi sakoma, kad diagrama yra y=cos(A+45 o) prieš diagrama y=cosA 45° kampu.
Tvarkaraštis. y=cos(A+45 o) (kosinusas).
Apskritai grafikas y=sin(A-α) atsilieka nuo y=sinA kampu α.
Kosinuso banga yra tokios pat formos kaip sinusoidė, bet prasideda 90 o į kairę, t.y. lenkia ją 90 o . Todėl cosA=sin(A+90o).
5 pavyzdys
Nubraižykite y=5sin(A+30o) intervale nuo A=0o iki A=360o
Sprendimas:
Amplitudė = 5, periodas = 360 o /1 = 360 o .
5sin(A+30 o) pirmauja 5sinA 30 o t.y. prasideda 30 o anksčiau.
Grafikas y=5sin(A+30 o) (sinusoidas).
6 pavyzdys
Nubraižykite y=7sin(2A-π/3) intervale nuo A=0 o iki A=360 o .
Sprendimas:
Amplitudė = 7, periodas = 2π/2= π radianai
Apskritai y=sin(pt-α) atsilieka nuo y=sinpt α/p, todėl 7sin(2A-π/3) atsilieka nuo 7sin2A (π/3)/2, t.y. už π/6 radianų arba 30 o
Leiskite ARBA pav. kairėje yra vektorius, laisvai besisukantis prieš laikrodžio rodyklę aplink O ω radianų/s greičiu. Besisukantis vektorius vadinamas fazės vektorius. Po t sekundžių OR pasisuks kampu ωt radianais (paveiksle kairėje tai kampas TOR). Jeigu ST statomas statmenai OR, tai sinωt=ST/OT, t.y. ST = OTsinωt.
Jei visi tokie vertikalūs komponentai yra projektuojami į y ir ωt diagramą, bus gauta sinusoidė su amplitudė OR.
Jei fazės vektorius ARBA padaro vieną apsisukimą (t. y. 2π radianus) per T sekundes, tai kampinis greitis ω=2π/T rad/s, iš kur
Т=2π/ ω (s), kur
T yra laikotarpį
Vadinamas pilnų laikotarpių, praeinančių per 1 sekundę, skaičius dažnis f.
Dažnis = (periodų skaičius)/(sekundė) = 1/ T = ω/2π Hz, tie. f= ω/2π Hz
Todėl kampinis greitis
ω=2πf rad/s.
Jei apskritai sinusoidinė funkcija atrodo taip y=sin(ωt± α), tada
A – amplitudė
ω – kampinis greitis
2π/ ω yra periodas T, s
ω/2π — dažnis f, Hz
α yra švino arba vėlavimo kampas (santykis su y=Аsinωt) radianais, jis taip pat vadinamas faziniu kampu.
7 pavyzdys
Kintamoji srovė pateikiama kaip i=20sin(90πt+0,26) amperų. Nustatykite amplitudę, periodą, dažnį ir fazės kampą (laipsniais)
Sprendimas:
i \u003d 20sin (90πt + 0,26) A, todėl
amplitudė yra 20 A
kampinis greitis ω= 90π, todėl
laikotarpis T= 2π/ ω = 2π/ 90π = 0,022 s = 22 ms
dažnis f\u003d 1 / T \u003d 1 / 0,022 \u003d 45,46 Hz
fazės kampas α= 0,26 rad. \u003d (0,26 * 180 / π) o \u003d 14,9 o.
8 pavyzdys
Virpesių mechanizmo didžiausias poslinkis yra 3 m, o dažnis - 55 Hz. Laike t=0 poslinkis yra 100 cm. Poslinkį išreikškite bendra forma Аsin(ωt± α).
Sprendimas
Amplitudė = didžiausias poslinkis = 3 m
Kampinis greitis ω=2πf = 2π(55) = 110 rad/s
Todėl poslinkis yra 3sin(110πt + α) m.
Esant t = 0 poslinkis = 100 cm = 1 m.
Todėl 1= 3sin(0 + α), t.y. sinα=1/3=0,33
Todėl α=arcsin0,33=19 o
Taigi poslinkis yra 3sin(110 πt + 0,33).
9 pavyzdys
Momentinės įtampos reikšmė kintamosios srovės grandinėje bet kuriomis t sekundėmis pateikiama kaip v=350sin(40πt-0,542)V. Rasti:
a) Amplitudė, periodas, dažnis ir fazės kampas (laipsniais)
b) įtampos reikšmė, kai t = 0
c) įtampos vertė esant t = 10 ms
d) laikas, per kurį įtampa pirmą kartą pasiekia 200 V.
Sprendimas:
a) Amplitudė 350 V, kampinis greitis ω=40π
Vadinasi,
laikotarpis Т=2π/ ω=2π/40π=0,05 s =50 ms
dažnis f=1/T=1/0,05=20 Hz
fazės kampas \u003d 0,542 rad (0,542 * 180 / π) \u003d 31 o su vėlavimu, palyginti su v \u003d 350sin (40πt)
b) Jei t \u003d 0, tada v \u003d 350sin (0-0,542) \u003d 350sin (-31 o) \u003d -180,25 V
c) Jei t \u003d 10 ms, tada v \u003d 350sin (40π10 / 10 3 -0,542) \u003d 350sin (0,714) \u003d 350sin41 o \u003d V 22
d) Jei v = 200 IR, tada 200 = 350 sin(40πt-0,542) 200/350 = sin(40πt-0,542)
Tvarkaraštis. Virpesių mechanizmas
(pavyzdys, sinusoidas).
v=350sin(40πt-0,542) Todėl (40πt-0,542)=arcsin200/350=35 o arba 0,611 rad.
40πt= 0,611+0,542=1,153.
Taigi, jei v = 200 V, laikas t = 1,153/40π = 9,179 ms
Straipsnio įvertinimas:
Funkcijų grafiko transformacija
Šiame straipsnyje supažindinsiu su tiesinėmis funkcijų grafikų transformacijomis ir parodysiu, kaip šias transformacijas naudoti norint gauti funkcijų grafiką iš funkcijų grafiko. 
Funkcijos tiesinė transformacija yra pačios funkcijos ir (arba) jos argumento pavertimas forma 
, taip pat transformaciją, kurioje yra argumento ir (arba) funkcijų modulis.
Dėl šių veiksmų daugiausia sunkumų braižant grafikus naudojant tiesines transformacijas:
- Bazinės funkcijos, iš tikrųjų, grafiko, kurio mes transformuojame, išskyrimas.
- Transformacijų eilės apibrėžimai.
IR Būtent ties šiais punktais mes ir gyvensime išsamiau.
Pažvelkime į funkciją atidžiau
Jis pagrįstas funkcija. Paskambinkime jai pagrindinė funkcija.
Braižydami funkciją atliekame bazinės funkcijos grafiko transformacijas .
Jei pakeistume funkciją ta pačia tvarka, kuria buvo nustatyta jo reikšmė tam tikrai argumento vertei, tada
Panagrinėkime, kokie linijinių argumentų ir funkcijų transformacijų tipai egzistuoja ir kaip jas atlikti.
Argumentų transformacijos.
1. f(x) f(x+b)
1. Sudarome funkcijos grafiką
2. Funkcijos grafiką perkeliame išilgai OX ašies |b| vienetų
- kairėje, jei b>0
- teisingai, jei b<0
Nubraižykime funkciją
1. Nubraižome funkciją
2. Pastumkite jį 2 vienetais į dešinę:
2. f(x) f(kx)
1. Sudarome funkcijos grafiką
2. Grafo taškų abscises padalinkite iš k, taškų ordinates palikite nepakitusias.
Nubraižykime funkciją.
1. Nubraižome funkciją
2. Visas grafiko taškų abscises padalykite iš 2, ordinates palikite nepakitusias:
3. f(x) f(-x)
1. Sudarome funkcijos grafiką
2. Rodome jį simetriškai apie OY ašį.
Nubraižykime funkciją.
1. Nubraižome funkciją
2. Rodome jį simetriškai apie OY ašį:
4. f(x) f(|x|)
1. Nubraižome funkciją
2. Ištriname grafiko dalį, esančią kairėje nuo OY ašies, grafiko dalį, esančią į dešinę nuo OY ašies Užpildome simetriškai apie OY ašį:
Funkcijos grafikas atrodo taip:
Nubraižykime funkciją
1. Sudarome funkcijų grafiką (tai funkcijos grafikas, perkeltas išilgai OX ašies 2 vienetais į kairę):
2. Diagramos dalis, esanti OY kairėje (x<0) стираем:
3. Grafiko dalis, esanti į dešinę nuo OY ašies (x>0), užpildoma simetriškai OY ašies atžvilgiu:
Svarbu! Dvi pagrindinės argumentų konvertavimo taisyklės.
1. Visos argumentų transformacijos atliekamos išilgai OX ašies
2. Visos argumento transformacijos atliekamos „atvirkščiai“ ir „atvirkščia tvarka“.
Pavyzdžiui, funkcijoje argumentų transformacijų seka yra tokia:
1. Paimame modulį iš x.
2. Pridėkite skaičių 2 prie modulo x.
Bet mes brėžėme atvirkštine tvarka:
Pirmiausia atlikome transformaciją 2. - grafiką perkėlėme 2 vienetais į kairę (tai yra taškų abscisės buvo sumažintos 2, tarsi "atvirkščiai")
Tada atlikome transformaciją f(x) f(|x|).
Trumpai tariant, transformacijų seka parašyta taip:
Dabar pakalbėkime apie funkcijų transformacija . Vykdomos transformacijos
1. Išilgai OY ašies.
2. Ta pačia seka, kuria atliekami veiksmai.
Tai yra transformacijos:
1. f(x)f(x)+D
2. Perkelkite jį išilgai OY ašies |D| vienetų
- aukštyn, jei D>0
- žemyn, jei D<0
Nubraižykime funkciją
1. Nubraižome funkciją
2. Perkelkite jį išilgai OY ašies 2 vienetais aukštyn:
2. f(x)Af(x)
1. Nubraižome funkciją y=f(x)
2. Visų grafiko taškų ordinates padauginame iš A, abscises paliekame nepakeistas.
Nubraižykime funkciją
1. Nubraižykite funkciją
2. Visų grafiko taškų ordinates padauginame iš 2:
3.f(x)-f(x)
1. Nubraižome funkciją y=f(x)
Nubraižykime funkciją.
1. Sudarome funkcijų grafiką.
2. Rodome jį simetriškai apie OX ašį.
4. f(x)|f(x)|
1. Nubraižome funkciją y=f(x)
2. Virš OX ašies esanti grafiko dalis paliekama nepakeista, grafiko dalis, esanti žemiau OX ašies, atvaizduojama simetriškai apie šią ašį.
Nubraižykime funkciją
1. Sudarome funkcijų grafiką. Jis gaunamas perkeliant funkcijos grafiką išilgai OY ašies 2 vienetais žemyn:
2. Dabar žemiau OX ašies esanti grafiko dalis bus rodoma simetriškai šios ašies atžvilgiu:
Ir paskutinė transformacija, kuri, griežtai tariant, negali būti vadinama funkcijos transformacija, nes šios transformacijos rezultatas nebėra funkcija:
|y|=f(x)
1. Nubraižome funkciją y=f(x)
2. Ištriname grafiko dalį, esančią žemiau OX ašies, tada grafo dalį, esančią virš OX ašies, užbaigiame simetriškai šiai ašiai.
Sukurkime lygties grafiką
1. Sudarome funkcijų grafiką:
2. Ištriname grafiko dalį, esančią žemiau OX ašies:
3. Virš OX ašies esanti grafiko dalis užbaigiama simetriškai apie šią ašį.
Ir pabaigai siūlau pažiūrėti VAIZDO PAMOKA, kurioje parodysiu nuoseklų funkcijų grafiko braižymo algoritmą
Šios funkcijos grafikas atrodo taip:
§ 11. Sinuso ir kosinuso grafikai | ||||||
Pakartokite: § 5. Laikrodis arba modernus trigonometrijos vaizdas. |
||||||
Nubraižykime funkciją y = sin x. Tuo pačiu mes vėl |
||||||
tinkamos valandos nuo § 5. | ||||||
Jei x = 0, tai akivaizdu, kad y = 0. Kai x | ||||||
lydosi nuo 0 iki π/2, skaičius sin x didėja nuo 0 iki | ||||||
1 (įsivaizduokite, kaip koordinatės | ||||||
rodyklės ant mūsų firminių laikrodžių). Sklypas | ||||||
x grafikas nuo 0 iki π/2 parodytas fig. 11.1. | ||||||
Mažo x atveju mūsų grafikas yra arti tiesės | ||||||
y = x: atminkite, kad mažam x | ||||||
apytikslė formulė sin x ≈ x. Galite pasakyti | ||||||
kad tiesė y = x yra kreivės su lygtimi liestinė | ||||||
y = sin x taške (0; 0). Taip pat atkreipkite dėmesį, kad mūsų diagramos dalis |
||||||
yra žemiau šios tiesės: juk smailiesiems kampams x, išmatuota |
||||||
radianais, sin x< x. | ||||||
Kuo x arčiau π/2, tuo plokštesnė mūsų kreivė. Tai |
||||||
atsiranda dėl to, kad rodyklės galo projekcija į y ašį, |
||||||
svyruojantis išilgai atkarpos [−1; 1], greičiausiai juda viduryje |
||||||
segmentą ir sulėtėja jo kraštuose: apie tai jau kalbėjome § 5. |
||||||
nuo π iki 3π / 2, sin x sumažėja nuo 0 iki -1, o kai x padidėja nuo 3π / 2 iki 2π, padidėja nuo -1 iki 0. Taigi, grafiko atkarpa 0 6 x 6 2π yra paruošta (pav. 11.2 b ). Beje, atkreipkite dėmesį, kad 11.2 pav. a kreivė yra simetriška vertikalios tiesės atžvilgiu su lygtimi x = π/2. Iš tiesų, redukcijos formulė sin(π/2 - x) = sin x rodo, kad taškai su abscisėmis x ir π - x turi tas pačias grafiko ordinates ir todėl yra simetriški tiesės x = π/ atžvilgiu. 2 (11.3 pav. A).
11.1 problema. Parašykite funkcijos y = sin x grafiko tiesės liestinės lygtį taške su koordinatėmis (π; 0).
11.2 pav. b kreivė yra centre simetriška taško su koordinatėmis (π; 0) atžvilgiu; tai išplaukia iš kitos redukcijos formulės: sin(2π - x) = - sin x (11.3 pav. b).
Kai turime funkcijos y \u003d sin x grafiko atkarpą 0 6 x 6 2π, visą grafiką jau lengva sudaryti. Iš tiesų, kai rodyklės galas nukeliauja keliu 2π, rodyklė grįžta į pradinę padėtį; judant į priekį viskas kartosis. Tai reiškia, kad grafikas sudarytas iš tų pačių dalių, kaip ir 11.2 pav. b. Galutinis funkcijos y = sin x grafikas atrodo kaip 11.4 pav. Tuo pačiu metu grafiko atkarpos ties x , , [−2π; 0]. . . gaunami iš 11.2 b paveikslo grafiko, pasislinkus išilgai x ašies 2π, 4π, −2π,. . . atitinkamai. Tai tik pakartotinis faktas, kad funkcijos y = sin x periodas yra 2π.
Ryžiai. 11.4. y = sinx.
Ryžiai. 11.5. y = cos x.
Dabar pavaizduokime funkciją y = cos x. Jį būtų galima sukurti taip pat, kaip mes sukūrėme sinuso grafiką. Tačiau pasirinksime kitą kelią, kuris leis panaudoti jau turimą informaciją.
Būtent, mes naudojame redukcijos formulę sin(x + π/2) = cos x. Šią formulę galima suprasti taip: funkcija y = cos x įgauna tas pačias reikšmes kaip ir funkcija y = sin x, bet π/2 anksčiau. Pavyzdžiui, funkcija y = sin x įgauna reikšmę 1, kai x = π/2, o funkcija y = cos x = sin(x + π/2) įgauna tą pačią reikšmę jau esant x = 0. Grafike, tai reiškia taip: kiekvieno grafo taškai y \u003d sin x yra grafiko taškas y \u003d cos x, kurio ordinatė yra ta pati, o abscisė yra π / 2 mažesnė (11.5 pav.). Todėl grafikas y = cos x bus gautas, jei grafikas y = sin x bus perkeltas išilgai x ašies π/2 į kairę. 11.5 paveiksle funkcijos y = cos x grafikas pavaizduotas kaip vientisa kreivė.
Taigi, mes išsiaiškinome, kad kosinuso grafikas gaunamas transformuojant
zacija (poslinkis) nuo sinuso grafiko. Atvejai, kai vienos funkcijos grafiką galima gauti transformuojant iš kitos funkcijos grafiko, yra įdomūs savaime, todėl apie juos pasakykime keletą žodžių.
Kaip, pavyzdžiui, atrodys funkcijos y = 2 sin x grafikas? Akivaizdu, kad šio grafiko taškų ordinatės gaunamos iš atitinkamų grafiko taškų y \u003d sin x ordinačių, padaugintų iš 2, todėl mūsų grafikas bus rodomas kaip vientisa kreivė Fig. 11.6. Galime sakyti, kad grafikas y = 2 sin x gaunamas iš grafiko y = sin x ištempus du kartus išilgai y ašies.
Ryžiai. 11.6. y = 2 sin x. | |||
Ryžiai. 11.7. y = sin 2x.
Dabar pavaizduokime funkciją y = sin 2x. Tai lengva suprasti
Ryžiai. 11.8. y = sin(2x + π/3).
kad funkcija y = sin 2x įgyja tas pačias reikšmes kaip ir funkcija y = sin x, bet su dvigubai didesnėmis x reikšmėmis. Pavyzdžiui, funkcija y = sin x įgauna reikšmę 1, kai x = π/2, o funkcija y = sin 2x jau esant x = π/4; kitaip tariant, norint gauti grafiką y = sin 2x, reikia perpus sumažinti visų grafiko taškų abscises y = sin x, o ordinates palikti nepakeistas. Kas atsitiks, parodyta fig. 11.7. Galima sakyti, kad grafikas y \u003d sin 2x (ištisinė linija 11.7 pav.) gaunamas iš grafiko y \u003d sin x 2 kartus susitraukiant iki y ašies.
Pabandykime nubraižyti ir funkciją y = sin(2x + π/3). Aišku, kad jis turi būti gautas tam tikra transformacija iš grafiko y = sin 2x. Iš pirmo žvilgsnio gali atrodyti, kad ši transformacija yra poslinkis į kairę π / 3 išilgai abscisių ašies, pagal analogiją su tuo, kas parodyta 11.5 pav. Tačiau jei taip būtų, tada, pavyzdžiui, paaiškėtų, kad funkcija y = sin(2x + π/3) įgyja reikšmę 1, kai x = π/4 − π/3 = π/12, kuri netiesa (patikrinkite!). Teisingas samprotavimas yra toks: sin(2x + π/3) = sin 2(x + π/6), taigi funkcija y = sin(2x+π/3) įgyja tas pačias reikšmes kaip ir funkcija y = sin 2x , bet π/6 anksčiau. Taigi poslinkis į kairę yra ne π / 3, o π / 6 (11.8 pav.).
Kreivės, kurios yra funkcijų y \u003d a sin bx grafikai, kur a 6 \u003d 0, b 6 \u003d 0, vadinamos sinusoidėmis. Atkreipkite dėmesį, kad „kosinuso“ kreivės įvesti nereikia: kaip matėme, kosinuso grafikas yra tokia pati kreivė, kaip ir sinuso grafikas, tik jis yra kitaip
naya koordinačių ašių atžvilgiu.
11.2 uždavinys. Kokios koordinatės taškų, pažymėtų pav. 11,8 klaustukų?
11.3 uždavinys. Paimkite žvakę, ploną popieriaus lapą ir aštrų peilį. Apvyniokite popieriaus lapą aplink žvakę keliais sluoksniais ir atsargiai peiliu įstrižai perpjaukite šią žvakę kartu su popieriumi. Dabar išskleiskite popierių. Pamatysite, kad jis buvo supjaustytas išilgai banguotos linijos. Įrodykite, kad ši banguota linija yra sinusoidė.
11.4 uždavinys. Nubraižykite funkcijų grafikus: | ||||||||||||||
d) y = 3 cos 2x; | ||||||||||||||
a) y = − sinx; b) | c) y = cos(x/2); | |||||||||||||
g) y = sin(πx). e) | ||||||||||||||
komentuoti. Jei trigonometrines funkcijas braižote ant languoto popieriaus, patogu pasirinkti šiek tiek kitokias mastelius išilgai ašių, kad sveikasis langelių skaičius atitiktų skaičių π ant x ašies. Pavyzdžiui, dažnai pasirenkama tokia skalė: išilgai ordinačių ašies 1 ilgio segmentas užima du langelius, išilgai abscisių ašies π ilgio segmentas užima 6 langelius.
11.5 uždavinys. Nubraižykite funkcijų grafikus:
a) y \u003d arcsin x; b) y = arckos x.
Pažiūrėkime, kaip grafikuose atrodo mums jau žinomi lygčių sin x = a ir cos x = a sprendiniai. Šie sprendiniai yra horizontalios tiesės y = a ir funkcijos grafiku y = sin x (atitinkamai y = cos x) susikirtimo taškų abscisės. Ant pav. 11.9 ,11.10 aiškiai matyti dvi sprendinių serijos, gautos ties −1< a < 1.
Sinuso ir kosinuso grafikai rodo, kokiais intervalais šios funkcijos didėja, o kokiais – mažėja. Pavyzdžiui, aišku, kad funkcija y = sin x didėja intervalais [−π/2; π/2],
